题目内容
已知点O(0,0),A(2,0),B(-4,0),C(a,a).若CO是∠ACB的平分线,则点C的坐标为 .
考点:一次函数综合题
专题:综合题
分析:根据题意画出图形,过O作OD⊥BC,OE⊥CE,再由CO平分∠ACB,利用角平分线定理得到OD=OE,表示出直线BC解析式,以及直线CE解析式,利用点到直线的距离公式列出关于a的方程,求出方程的解得到a的值,即可确定出C坐标.
解答: 解:根据题意画出图形,过O作OD⊥BC,OE⊥CE,
解:根据题意画出图形,过O作OD⊥BC,OE⊥CE,
∵CO平分∠ACB,
∴OD=OE,
∵B(-4,0),C(a,a),
∴直线BC解析式为y=
(x+4)=
(x+4),即ax-(a+4)y+4a=0,
∵A(2,0),C(a,a),
∴直线AC解析式为y=
(x-2),即ax-(a-2)y-2a=0,
∴
=
,
整理得:a(a-4)=0,
解得:a=0或a=4,
当a=0时,C与原点重合,舍去;
∴a=4,
则C坐标为(4,4).
故答案为:(4,4)
 解:根据题意画出图形,过O作OD⊥BC,OE⊥CE,
解:根据题意画出图形,过O作OD⊥BC,OE⊥CE,∵CO平分∠ACB,
∴OD=OE,
∵B(-4,0),C(a,a),
∴直线BC解析式为y=
| a-0 |
| a+4 |
| a |
| a+4 |
∵A(2,0),C(a,a),
∴直线AC解析式为y=
| a-0 |
| a-2 |
∴
| |4a| | ||
|
| |-2a| | ||
|
整理得:a(a-4)=0,
解得:a=0或a=4,
当a=0时,C与原点重合,舍去;
∴a=4,
则C坐标为(4,4).
故答案为:(4,4)
点评:此题属于一次函数解析式,涉及的知识有:待定系数法确定一次函数解析式,角平分线定理,点到直线的距离公式,坐标与图形性质,熟练掌握点到直线的距离公式是解本题的关键.

练习册系列答案
相关题目
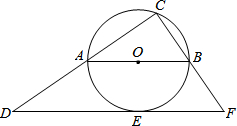 如图,AB为⊙O的直径,C为⊙O上一点,DF切⊙O于E点,分别与CA、CB的延长线于点D、F,已知AB∥DF,CD=4,CF=3,则AC=( )
如图,AB为⊙O的直径,C为⊙O上一点,DF切⊙O于E点,分别与CA、CB的延长线于点D、F,已知AB∥DF,CD=4,CF=3,则AC=( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,反比例函数y=
如图,反比例函数y=