题目内容
已知点A（x1，y1）、B（x2，y2）为函数y=-2（x-1）2+3的图象上的两点，若x1＞x2＞1，则y1 y2．
考点：二次函数图象上点的坐标特征
专题：
分析：先根据函数解析式确定出对称轴为直线x=1，再根据二次函数图象上的点，x＞1时，y随x的增大而减小解答．
解答：解：∵y=-2（x-1）2+3，
∴抛物线的开口向下，二次函数图象的对称轴为直线x=1，
∵x1＞x2＞1，
∴y1＜y2．
故答案为：＜．
∴抛物线的开口向下，二次函数图象的对称轴为直线x=1，
∵x1＞x2＞1，
∴y1＜y2．
故答案为：＜．
点评：本题考查了二次函数图象上点的坐标特征，主要利用了二次函数的增减性，求出对称轴解析式是解题的关键．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知实数（x2-x）2-4（x2-x）-12=0，则代数式x2-x+1的值为（ ）
| A、-1 | B、7 |
| C、-1或7 | D、以上全不正确 |
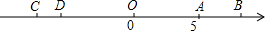如图，数轴上有两条线段AB和CD，线段AB的长度为4个单位，线段CD的长度为2个单位，点A在数轴上表示的数是5，且A、D两点之间的距离为11．