题目内容
15. 如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,∠ACB=90°.若AF=4,CF=1.则BD的长是$\frac{5}{3}$.
如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,∠ACB=90°.若AF=4,CF=1.则BD的长是$\frac{5}{3}$.
分析 设BD=x,由切线长定理可得BE=BD=x,AD=AF=4,CE=CF=1,因为△ACB是直角三角形,所以可根据勾股定理建立关于x的方程,解方程即可.
解答 解:
设BD=x,
∵Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,
∴得BE=BD=x,AD=AF=4,CE=CF=1,
∵∠ACB=90°,
∴AC2+BC2=AB2,
即52+(x+1)2=(4+x)2,
解得:x=$\frac{5}{3}$,
故答案为:$\frac{5}{3}$.
点评 本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.同时也考查了切线长定理以及勾股定理的运用.

练习册系列答案
相关题目
3. 如图,在同一平面内直线l∥m∥n,直线AB与直线l,m,n分别交于A,B,C三点,AB=BC,D为直线m上一点,∠ABD=40°,∠BAD=70°,若直线n上有一点E,BE=AD,则∠CEB的度数为( )
如图,在同一平面内直线l∥m∥n,直线AB与直线l,m,n分别交于A,B,C三点,AB=BC,D为直线m上一点,∠ABD=40°,∠BAD=70°,若直线n上有一点E,BE=AD,则∠CEB的度数为( )
 如图,在同一平面内直线l∥m∥n,直线AB与直线l,m,n分别交于A,B,C三点,AB=BC,D为直线m上一点,∠ABD=40°,∠BAD=70°,若直线n上有一点E,BE=AD,则∠CEB的度数为( )
如图,在同一平面内直线l∥m∥n,直线AB与直线l,m,n分别交于A,B,C三点,AB=BC,D为直线m上一点,∠ABD=40°,∠BAD=70°,若直线n上有一点E,BE=AD,则∠CEB的度数为( )| A. | 40°或70° | B. | 70° | C. | 110° | D. | 70°或110° |
4.下列命题中,假命题是( )
| A. | 两条直角边对应相等的两个直角三角形全等 | |
| B. | 有一个角是60°的等腰三角形是等边三角形 | |
| C. | 顶角相等的两个等腰三角形全等 | |
| D. | 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边分别相等,那么这两个直角三角形全等 |
 如图,在△ABC中,点D、E分别在AB,AC边上,DE∥BC.若AE:EC=3:1,AD=6,则BD等于( )
如图,在△ABC中,点D、E分别在AB,AC边上,DE∥BC.若AE:EC=3:1,AD=6,则BD等于( )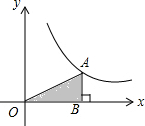 如图,已知双曲线y=$\frac{4}{x}$上有一点A,过A作AB垂直x轴于点B,连接OA,则△AOB的面积为( )
如图,已知双曲线y=$\frac{4}{x}$上有一点A,过A作AB垂直x轴于点B,连接OA,则△AOB的面积为( )