题目内容
7. 如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EF的长为$\sqrt{5}$.
如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EF的长为$\sqrt{5}$.
分析 如图,AC交EF于点O,由勾股定理先求出AC的长度,根据折叠的性质可判断出RT△EOC~RT△ABC,从而利用相似三角形的对应边成比例可求出OE,再由EF=2OE可得出EF的长度
解答 解:如图所示,AC交EF于点O,
由勾股定理知AC=2$\sqrt{5}$,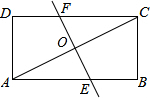
又∵折叠矩形使C与A重合时有EF⊥AC,
则Rt△AOE∽Rt△ABC,
∴$\frac{OE}{BC}=\frac{AO}{AB}$,
∴OE=$\frac{\sqrt{5}}{2}$
故EF=2OE=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 此题考查了翻折变换、勾股定理及矩形的性质,难度一般,解答本题的关键是判断出Rt△AOE∽Rt△ABC,利用相似三角形的性质得出OE的长.

练习册系列答案
相关题目
18. 如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EF的长为( )
如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EF的长为( )
 如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EF的长为( )
如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,若AB=4,BC=2,那么线段EF的长为( )| A. | 2$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | $\frac{4\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{5}$ |
2.下列说法正确的是( )
| A. | 掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件 | |
| B. | 甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定 | |
| C. | “明天降雨的概率为$\frac{1}{2}$”,表示明天有半天都在降雨 | |
| D. | 了解一批电视机的使用寿命,适合用普查的方式 |
 在一海岸直线a上由于A、B两个海港,一轮船由B港沿北偏东60°方向航行,当轮船航行20海里到达P处时,在A港测得轮船在A港的北偏西60°方向;当轮船继续按原航线航行到C处时,在A港测得轮船在A港的北偏东15°方向上.此时轮船在C处发生故障,准备返回到A港维修,求AC的距离(保留根号).
在一海岸直线a上由于A、B两个海港,一轮船由B港沿北偏东60°方向航行,当轮船航行20海里到达P处时,在A港测得轮船在A港的北偏西60°方向;当轮船继续按原航线航行到C处时,在A港测得轮船在A港的北偏东15°方向上.此时轮船在C处发生故障,准备返回到A港维修,求AC的距离(保留根号).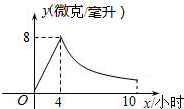 某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).


