题目内容
8.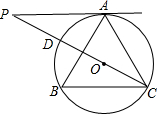 如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点P,CP交⊙O于点D,若AC=3,则△APC的面积为( )
如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点P,CP交⊙O于点D,若AC=3,则△APC的面积为( )| A. | 3$\sqrt{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{3}{2}$$\sqrt{3}$ | D. | $\frac{9}{4}$$\sqrt{3}$ |
分析 连接OA,作AH⊥PC于H,如图,根据圆周角定理得到∠AOC=2∠B=120°,则利用等腰三角形的性质和三角形内角和得到∠OAC=∠OCA=30°,再利用切线的性质得∠OAP=90°,则∠CAP=120°,所以∠P=30°,利用等腰三角形的性质得PH=CH,然后计算出AH和CH,最后利用三角形面积公式计算.
解答 解:连接OA,作AH⊥PC于H,如图,则∠AOC=2∠B=120°,
∵OA=OC,
∴∠OAC=∠OCA=30°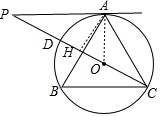
∵PA为切线,
∴OA⊥PA,
∴∠OAP=90°,
∴∠CAP=120°,
∴∠P=30°,
∴△PAC为等腰三角形,
∵PH⊥PC,
∴PH=CH,
在Rt△ACH中,AH=$\frac{1}{2}$AC=$\frac{3}{2}$,
CH=$\sqrt{3}$AH=$\frac{3\sqrt{3}}{2}$,
∴PC=3$\sqrt{3}$,
∴△APC的面积=$\frac{1}{2}$•3$\sqrt{3}$•$\frac{3}{2}$=$\frac{9\sqrt{3}}{4}$.
故选D.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
18.解方程$\frac{3x+2}{4}$-$\frac{5x+1}{12}$=1-$\frac{2x-1}{2}$时,去分母正确的是( )
| A. | 3(3x+2)-5x+1=12-6(2x-1) | B. | 3(3x+2)-5x-1=1-6(2x-1) | ||
| C. | 3(3x+2)-5x-1=12-6(2x-1) | D. | (3x+2)-5x+1=12-6(2x-1) |
19.下列命题中,正确的个数是( )
①半径相等的两个圆是等圆;②一条弦把圆分成的两段弧中,至少有一条是优弧;③任何一个三角形只有一个外接圆;④内心到三角形各顶点的距离相等.
①半径相等的两个圆是等圆;②一条弦把圆分成的两段弧中,至少有一条是优弧;③任何一个三角形只有一个外接圆;④内心到三角形各顶点的距离相等.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.如果向东走2km记作+2km,那么-3km表示( )
| A. | 向东走3km | B. | 向西走3km | C. | 向南走3km | D. | 向北走3km |
3.下列说法正确的是( )
| A. | 若ac=bc,则a=b | B. | 若$\frac{a}{c}$=$\frac{b}{c}$,则a=b | C. | 若$\frac{a}{2}$=$\frac{b}{4}$,则a=2b | D. | 若a2=b2,则a=b |
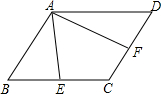 如图,在平行四边形ABCD中,E,F分别是BC,CD的中点,AE=3,AF=4,∠EAF=60°,则BC边上的高是$\frac{12\sqrt{3}}{7}$.
如图,在平行四边形ABCD中,E,F分别是BC,CD的中点,AE=3,AF=4,∠EAF=60°,则BC边上的高是$\frac{12\sqrt{3}}{7}$. 如图,某物体在20秒内的速度与时间的关系图,物体最高速度为20厘米/秒.
如图,某物体在20秒内的速度与时间的关系图,物体最高速度为20厘米/秒.