题目内容
4.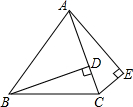 如图,在△ABC中,AC=BC,BD⊥AC于点D,在△ABC外作∠CAE=∠CBD,过点C作CE⊥AE于点E.如果∠BCE=140°,求∠BAC的度数.
如图,在△ABC中,AC=BC,BD⊥AC于点D,在△ABC外作∠CAE=∠CBD,过点C作CE⊥AE于点E.如果∠BCE=140°,求∠BAC的度数.
分析 由垂直的定义得到两个角为直角,再由已知角相等,利用两对角相等的三角形相似得到三角形BDC与三角形AEC相似,利用相似三角形对应角相等求出∠BCD度数,再由AC=BC,利用等边对等角得到一对角相等,求出所求角度数即可.
解答 解:∵BD⊥AC,CE⊥AE,
∴∠BDC=∠E=90°,
∵∠CAE=∠CBD,
∴△BDC∽△AEC,
∴∠BCD=∠ACE,
∵∠BCE=140°,
∴∠BCD=∠ACE=70°,
∵AC=BC,
∴∠ABC=∠BAC=55°.
点评 此题考查了相似三角形的判定与性质,以及等腰三角形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
15.九年级一班有七个学习小组,每组人数如下:5,5,6,x,6,7,8,已知平均每个小组有6个,则这组数据的众数与中位数分别是( )
| A. | 5,6 | B. | 6,5 | C. | 6,7 | D. | 5,8 |
16.如果向东走2km记作+2km,那么-3km表示( )
| A. | 向东走3km | B. | 向西走3km | C. | 向南走3km | D. | 向北走3km |
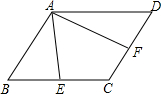 如图,在平行四边形ABCD中,E,F分别是BC,CD的中点,AE=3,AF=4,∠EAF=60°,则BC边上的高是$\frac{12\sqrt{3}}{7}$.
如图,在平行四边形ABCD中,E,F分别是BC,CD的中点,AE=3,AF=4,∠EAF=60°,则BC边上的高是$\frac{12\sqrt{3}}{7}$. 如图,在△ABC中,点D,E分别在边AB,AC上,若∠ADE=∠ABC;AD=3,AB=5,DE=2,求BC.
如图,在△ABC中,点D,E分别在边AB,AC上,若∠ADE=∠ABC;AD=3,AB=5,DE=2,求BC.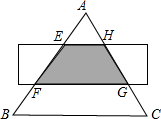 如图,△ABC是面积为18cm2的等边三角形,被一长边平行于BC的矩形所截,AB被截成三等份,则图中阴影部分的面积为6 cm2.
如图,△ABC是面积为18cm2的等边三角形,被一长边平行于BC的矩形所截,AB被截成三等份,则图中阴影部分的面积为6 cm2.