题目内容
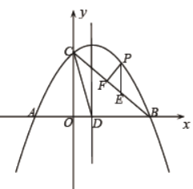
【题目】如图所示,直线![]() 与坐标轴交于点
与坐标轴交于点![]() ,与抛物线
,与抛物线![]() 交于点
交于点![]() ,点
,点![]() 的坐标是
的坐标是![]() .
.
(1)求抛物线的解析式;
(2)若点![]() 是线段
是线段![]() 上(不与
上(不与![]() 重合)的一个动点,过点
重合)的一个动点,过点![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,过点
,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,以
,以![]() 为边作矩形
为边作矩形![]() ,请求出矩形
,请求出矩形![]() 周长的最大值;
周长的最大值;
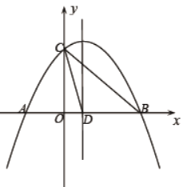
(3)若点![]() 在
在![]() 轴正半轴上,当
轴正半轴上,当![]() 恰好是等腰三角形时,请直接写出点
恰好是等腰三角形时,请直接写出点![]() 的坐标.
的坐标.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]()
【解析】
(1)对于![]() ,令y=0求出x=-2即可得点A(-2,0),把A,C点坐标代入
,令y=0求出x=-2即可得点A(-2,0),把A,C点坐标代入![]() 求出a,c的值即可;
求出a,c的值即可;
(2)设点D的坐标是![]() ,则点E的坐标是
,则点E的坐标是![]() ,可得DE=
,可得DE=![]() ,证明△DFE∽△BOA,得DF∶EF∶DE =3∶4∶5.从而可得矩形DFEG的周长
,证明△DFE∽△BOA,得DF∶EF∶DE =3∶4∶5.从而可得矩形DFEG的周长![]() ,从而可得结论;
,从而可得结论;
(3)由勾股定理求出AC=![]() ,设P(0,m)(m>0),然后分AP=AC,AC=PC,AP=PC三种情况列式求解即可.
,设P(0,m)(m>0),然后分AP=AC,AC=PC,AP=PC三种情况列式求解即可.
解:(1)由![]() 知,y=0时x=-2,
知,y=0时x=-2,
∴A(-2,0).
∵抛物线![]() 经过A(-2,0) 、C(4,
经过A(-2,0) 、C(4,![]() )两点,
)两点,
∴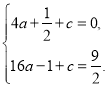 解得
解得
∴抛物线的解析式为![]() .
.
(2)∵DE∥y轴,点D在线段AC上,点E在抛物线上,
∴设点D的坐标是![]() ,则点E的坐标是
,则点E的坐标是![]() .
.
∴DE=![]() .
.
由![]() 知A(-2,0),B(0,
知A(-2,0),B(0, ![]() ),
),
∴AO=2,OB=![]()
Rt△OAB中,由勾股定理可得,AB=![]()
∴OB∶OA∶AB =3∶4∶5.
由题意得,∠DFE=∠BOA=90°,∠EDF=∠ABO,
∴△DFE∽△BOA.
∴DF∶EF∶DE =3∶4∶5.
∴矩形DFEG的周长![]() ,其中
,其中![]() .
.
∴当![]() 时,矩形DFEG的周长取得最大值
时,矩形DFEG的周长取得最大值![]() .
.
(3)由题意得,![]() ,
,![]() ,
,
设![]() ,
,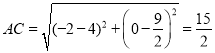
①若![]() ,则
,则![]()
![]()
![]()
![]() 或
或![]() (舍去)
(舍去)
②若![]() ,则
,则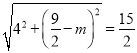
![]()
![]()
![]() 或
或![]() (负值舍去)
(负值舍去)
③若![]() ,则
,则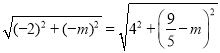
![]()
![]()
综上所述,点P的坐标为![]() ,
,![]() ,
,![]() .
.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目