Question

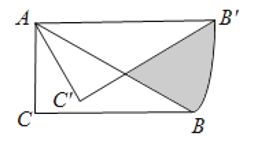
【题目】如图，在中，，，．将绕点逆时针旋转得到，则图中阴影部分的面积是______．

Answer 1

【答案】

【解析】

令AB与B′C′交于点D，根据三角函数求出AC=1，∠BAC=60°，即可得到AB=2，∠ABC=30°，再根据旋转的性质得到AC′=AC=1，AB′=AB=2，B′C′=BC=，∠B′AB=30°，∠C′AB′=∠CAB=60°，则∠C′AD=∠C′AB′∠BAB′=30°，接着在Rt△AC′D中，利用∠C′AD=30°可得C′D，从而求出 B′D，然后根据三角形面积公式、扇形面积公式进行计算即可．

解：∵∠C=90°，，，

∴∠BAC=60°，AC=1，

∴∠ABC=30°，即AB=2AC=2，

令AB与B′C′交于点D，

∵Rt△ABC绕点A逆时针旋转30°后得到△AB′C′，
∴AC′=AC=1，AB′=AB=2，B′C′=BC=，∠B′AB=30°，∠C′AB′=∠CAB=60°，
∴∠C′AD=∠C′AB′-∠BAB′=60°-30°=30°，
在Rt△AC′D中，∵∠C′AD=30°，
∴C′D=，
∴B′D=B′C′-C′D=，
∴图中阴影部分的面积=S扇形BAB′-S△ADB′ ．
故答案为：．