题目内容
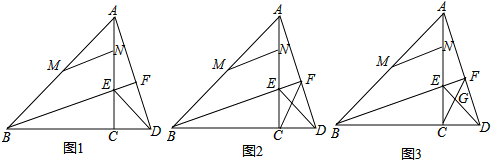
点D为Rt△ACB边BC延长线上一点,点E在边AC上,点M、N分别为线段AB、AE的中点,连接DE、DA,∠ACB=90°,∠B=∠CED.
(1)若∠B=45°,如图1,求证:MN=
AD;
(2)在(1)的条件下,连接BE并延长BE交线段AD于点F,连接FC,如图2,请你判断线段FE、FC与线段FD之间的数量关系为 ;
(3)在(2)的条件下,如图3,连接DE交FC于点G,若MN:DE=
:2,四边形MNEB的面积为
,求GE的长.
(1)若∠B=45°,如图1,求证:MN=
| 1 |
| 2 |
(2)在(1)的条件下,连接BE并延长BE交线段AD于点F,连接FC,如图2,请你判断线段FE、FC与线段FD之间的数量关系为
(3)在(2)的条件下,如图3,连接DE交FC于点G,若MN:DE=
| 5 |
| 9 |
| 2 |

考点:相似三角形的判定与性质,全等三角形的判定与性质
专题:压轴题
分析:(1)根据已知条件求得BC=AC,CE=CD,然后证明△BCE≌△ACD得出BE=AD,因为MN是三角形ABE的中位线,MN=
BE,所以MN=
AD;
(2)先证得A、B、C、F共圆,再证△AEB∽△FEC,△FCD∽△BDA,得出FE=
•FC,FD=
•FC,因为AE+BD=AC-EC+BC+CD=2AC,AB=
AC,所以
=
=
=
,进而证得FE+FD=
•FC=
•FC=
•FC=
FC=
FC;
(3)根据MN:DE=
:2,设MN=
a,DE=2a,进而求得BE=2
a,EC=
a,BC=3
a,根据三角形面积的比等于相似比的平方结合四边形MNEB的面积为
,求得a=1,进而求得BE=2
,EC=CD=
,BC=3
,ED=2,AE=2
,EF=
,AF=
,DF=
,通过△AEF∽△ADC,得出AE:AF=AD:AC,再根据对应边成比例且夹角相等的三角形相似证得△AED∽△AFC,得出∠ACF=∠ADE,进而得出∠CEG=∠CFD=45°,∠EFC=45°,作EP⊥FC,DQ⊥FC,根据勾股定理求得EP,DQ的长,最后根据△EGP∽△DGQ,对应边成比例即可求得GE的长.
| 1 |
| 2 |
| 1 |
| 2 |
(2)先证得A、B、C、F共圆,再证△AEB∽△FEC,△FCD∽△BDA,得出FE=
| AE |
| AB |
| BD |
| AB |
| 2 |
| AE+BD |
| AB |
| 2AC |
| AB |
| 2AC | ||
|
| 2 |
| AE+BD |
| AB |
| 2AC |
| AB |
| 2AC | ||
|
| 2 |
| 2 |
(3)根据MN:DE=
| 5 |
| 5 |
| 5 |
| 2 |
| 2 |
| 9 |
| 2 |
| 5 |
| 2 |
| 2 |
| 2 |
2
| ||
| 5 |
6
| ||
| 5 |
4
| ||
| 5 |
解答:解:(1)∵∠ACB=90°,∠B=∠CED,∠B=45°,
∴BC=AC,CE=CD,
在△BCE和△ACD中,
,
∴△BCE≌△ACD(SAS),
∴BE=AD,
∵点M、N分别为线段AB、AE的中点,
∴MN=
BE,
∴MN=
AD;
(2)∵△BCE≌△ACD,
∴∠CBE=∠EAF,
∵∠BEC=∠AEF,
∴∠AFB=∠ACB=90°,
∴A、B、C、F共圆,
∴∠ABF=∠ACF,
∵∠AEB=∠FEC,
∴△AEB∽△FEC,
∴FE:AE=FC:AB,
∴FE=
•FC,
∵∠BAF+∠ABF=90°,∠FCD+∠ACF=90°,
∴∠FCD=∠BAD,
∵∠FDC=∠BDA,
∴△FCD∽△BDA,
∴FD:BD=FC:AB,
∴FD=
•FC
∴FE+FD=
•FC,
∵AC=BC,CE=CD,
∴AE+BD=AC-EC+BC+CD=2AC,
∵在RT△ABC中,AB=
AC,
∴
=
=
=
,
∴FE+FD=
FC;
(3)∵MN:DE=
:2,
∴设MN=
a,DE=2a,
∴BE=2MN=2
a,EC=
ED=
a,
∴BC=
=3
a,
∵MN=
BE,
∴
=
,
∴
=
,
又∵四边形MNEB的面积为
,
∴S△ABE=6,
∵S△BCE=
BC•EC=
×3
a×
a=3a2,S△ABC=
BC2=9a2,S△ABE+S△BCE=S△ABC,
∴6+3a2=9a2,解得:a=1,
∴BE=2
,EC=CD=
,BC=3
,ED=2,
∴AE=2
,EF=
,AF=
,DF=
,
∵∠AFE=∠ACD=90°,∠EAF=∠DAC,
∵△AEF∽△ADC,
∴AE:AF=AD:AC,
∵∠FAC=∠EAD,
∴△AED∽△AFC,
∴∠ACF=∠ADE,
∴∠CEG=∠CFD=45°,
∵∠BFD=90°,
∴∠EFC=45°,
作EP⊥FC,DQ⊥FC
∴EP=
EF=
×
=
,DQ=
DF=
×
=
,
∴△EGP∽△DGQ,
∴EP:DQ=EG:DG=1:2,
∴EG=
ED=
×2=
,
所以EG=
;
∴BC=AC,CE=CD,
在△BCE和△ACD中,
|
∴△BCE≌△ACD(SAS),
∴BE=AD,
∵点M、N分别为线段AB、AE的中点,
∴MN=
| 1 |
| 2 |
∴MN=
| 1 |
| 2 |
(2)∵△BCE≌△ACD,
∴∠CBE=∠EAF,
∵∠BEC=∠AEF,
∴∠AFB=∠ACB=90°,
∴A、B、C、F共圆,
∴∠ABF=∠ACF,
∵∠AEB=∠FEC,
∴△AEB∽△FEC,
∴FE:AE=FC:AB,
∴FE=
| AE |
| AB |
∵∠BAF+∠ABF=90°,∠FCD+∠ACF=90°,
∴∠FCD=∠BAD,
∵∠FDC=∠BDA,
∴△FCD∽△BDA,
∴FD:BD=FC:AB,
∴FD=
| BD |
| AB |
∴FE+FD=
| AE+BD |
| AB |
∵AC=BC,CE=CD,
∴AE+BD=AC-EC+BC+CD=2AC,
∵在RT△ABC中,AB=
| 2 |
∴
| AE+BD |
| AB |
| 2AC |
| AB |
| 2AC | ||
|
| 2 |
∴FE+FD=
| 2 |
(3)∵MN:DE=
| 5 |
∴设MN=
| 5 |
∴BE=2MN=2
| 5 |
| ||
| 2 |
| 2 |
∴BC=
| BE2-EC2 |
| 2 |
∵MN=
| 1 |
| 2 |
∴
| S△AMN |
| S△ABE |
| 1 |
| 4 |
∴
| S△AMN |
| S四边形MNEB |
| 1 |
| 3 |
又∵四边形MNEB的面积为
| 9 |
| 2 |
∴S△ABE=6,
∵S△BCE=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
∴6+3a2=9a2,解得:a=1,
∴BE=2
| 5 |
| 2 |
| 2 |
∴AE=2
| 2 |
2
| ||
| 5 |
6
| ||
| 5 |
4
| ||
| 5 |
∵∠AFE=∠ACD=90°,∠EAF=∠DAC,
∵△AEF∽△ADC,
∴AE:AF=AD:AC,
∵∠FAC=∠EAD,
∴△AED∽△AFC,
∴∠ACF=∠ADE,
∴∠CEG=∠CFD=45°,
∵∠BFD=90°,
∴∠EFC=45°,
作EP⊥FC,DQ⊥FC
∴EP=
| ||
| 2 |
| ||
| 2 |
2
| ||
| 5 |
| ||
| 5 |
| ||
| 2 |
| ||
| 2 |
4
| ||
| 5 |
2
| ||
| 5 |
∴△EGP∽△DGQ,
∴EP:DQ=EG:DG=1:2,
∴EG=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
所以EG=
| 2 |
| 3 |
点评:本题考查了三角形全等的判定和性质、三角形的中位线定理、三角形相似的判定和性质、等腰直角三角形的性质、勾股定理的应用等,本题的关键是熟练掌握三角形全等的性质定理和判定定理以及三角形相似的判定定理.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 如图,在?ABCD中,E,F为BC上两点,且BE=CF,AF=DE.求证:?ABCD是矩形.
如图,在?ABCD中,E,F为BC上两点,且BE=CF,AF=DE.求证:?ABCD是矩形.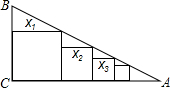 如图:Rt△ABC中,∠C=90°,BC=1,AC=2,把边长分为x1,x2,x3,…xn的n个正方形依次放在△ABC中,则xn=
如图:Rt△ABC中,∠C=90°,BC=1,AC=2,把边长分为x1,x2,x3,…xn的n个正方形依次放在△ABC中,则xn=