题目内容
如图，在?ABCD中，E，F为BC上两点，且BE=CF，AF=DE．求证：?ABCD是矩形．考点：矩形的判定
专题：证明题
分析：首先证得△ABF≌△DCE，从而证得∠B=∠C，然后利用平行四边形的对边平行得到两个角均为直角，从而利用有一个角是直角的平行四边形是矩形判定即可．
解答：证明：∵四边形ABCD为平行四边形，
∴AB=CD，
∵BE=CF，
∴BF=CE，
在△ABF和△DCE中，
，
∴△ABF≌△DCE（SSS），
∴∠B=∠C，
∵AB∥CD，
∴∠B=∠C=90°，
∴?ABCD是矩形．
∴AB=CD，
∵BE=CF，
∴BF=CE，
在△ABF和△DCE中，
|
∴△ABF≌△DCE（SSS），
∴∠B=∠C，
∵AB∥CD，
∴∠B=∠C=90°，
∴?ABCD是矩形．
点评：考查了矩形的判定，解题的关键是了解矩形的判定定理，难度不大．
练习册系列答案
阅读快车系列答案
相关题目
在如图边长为7.6的正方形的角上挖掉一个边长为2.6的小正方形．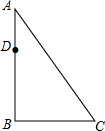
如图，AB为一棵大树，在树上距地面10m的D处有两只猴子，它们同时发现地面上的C处有一筐水果，一只猴子从D处上爬到树顶A处，利用拉在A处的滑绳AC，滑到C处，另一只猴子从D处滑到地面B，再由B跑到C，已知两猴子所经路程都是30m，求树高AB．