Question

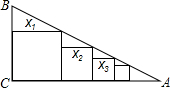如图：Rt△ABC中，∠C=90°，BC=1，AC=2，把边长分为x₁，x₂，x₃，…x_n的n个正方形依次放在△ABC中，则x_n=

 

．

Answer 1

考点：相似三角形的判定与性质,正方形的性质

专题：

分析：由四边形CDEF是正方形，即可得CD=CF=DE=EF=x₁，DE∥AC，然后根据平行线分线段成比例定理，即可得

DE

AC

，又由BC=1，AC=2，即可求得x₁的值，同理求得x₂，x₃的值；
观察规律即可求得第n个正方形的边长x_n=（

2

3

）ⁿ．

解答：解：如图，

∵四边形CDEF是正方形，
则CD=CF=DE=EF=x₁，DE∥AC，
∴

DE

AC

=

BD

BC

，
即

x1

1

=

2-x1

2

∴x1=

2

3

同理：x2=(

2

3

)2，
x3=(

2

3

)3，
…
∴xn=(

2

3

)n．
故答案为：（

2

3

）ⁿ．

点评：此题考查了正方形的性质，平行线分线段成比例定理，考查了学生的观察归纳能力．此题难度适中，解题的关键是数形结合思想与方程思想的应用．