题目内容
4. 如图,一个数阵,每行和每列元素个数都是无限的,但是我们可以按照以下规律,将每个元素都标序(以下右边是数阵中的元素,左边是其序号):1←→a${\;}_{1}^{1}$,2←→a${\;}_{2}^{1}$,3←→a${\;}_{1}^{2}$,4←→a${\;}_{3}^{1}$,5←→a${\;}_{2}^{2}$,6←→a${\;}_{1}^{3}$,7←→a${\;}_{4}^{1}$,…,11←→a${\;}_{5}^{1}$,…,按此规律填写下列空格:18←→${a}_{3}^{3}$,80←→a${\;}_{12}^{2}$.
如图,一个数阵,每行和每列元素个数都是无限的,但是我们可以按照以下规律,将每个元素都标序(以下右边是数阵中的元素,左边是其序号):1←→a${\;}_{1}^{1}$,2←→a${\;}_{2}^{1}$,3←→a${\;}_{1}^{2}$,4←→a${\;}_{3}^{1}$,5←→a${\;}_{2}^{2}$,6←→a${\;}_{1}^{3}$,7←→a${\;}_{4}^{1}$,…,11←→a${\;}_{5}^{1}$,…,按此规律填写下列空格:18←→${a}_{3}^{3}$,80←→a${\;}_{12}^{2}$.
分析 根据元素和序号间的关系可得出和为n的数有n-1个,根据18=1+2+3+4+5+3即可得出序号为18的元素为${a}_{3}^{3}$,进而即可得出元素为a${\;}_{12}^{2}$的序号为1+2+3+…+12+2=80,此题得解.
解答 解:∵2=1+1,
∴和为2的数只有1个;
∵3=1+2=2+1,
∴和为3的数有2个;
∵4=1+3=2+2=3+1,
∴和为4的数只有3个;
∴和为5的数只有4个,和为6的数只有5个,…,和为n的数有n-1个.
∵18=1+2+3+4+5+3,
∴序号为18的数为和为6的第3个数,即18←→${a}_{3}^{3}$.
∵2+12=14,和为13的数有12个,
∴元素a${\;}_{12}^{2}$的序号为1+2+3+…+12+2=$\frac{12×(1+12)}{2}$+2=80.
故答案为:${a}_{3}^{3}$;80.
点评 本题考查了规律型中的数字与图形的变化类,根据数阵中元素与序号的变化找出变化规律是解题的关键.

练习册系列答案
相关题目
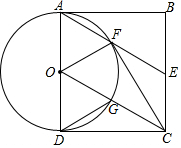 如图,正方形ABCD,E为BC边的中点,连接AE、OC,以AD为直径的⊙O交AE于点F,交OC于点G,连接CF,DG.
如图,正方形ABCD,E为BC边的中点,连接AE、OC,以AD为直径的⊙O交AE于点F,交OC于点G,连接CF,DG.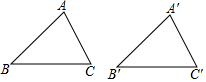 ①已知AB=A′B′,BC=B′C′,那只要再知道∠B=∠B′,就可以根据“SAS”得到△ABC≌△A′B′C′.
①已知AB=A′B′,BC=B′C′,那只要再知道∠B=∠B′,就可以根据“SAS”得到△ABC≌△A′B′C′.