题目内容
19.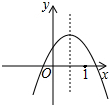 已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论:
已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则下列结论:①abc<0;②b2>4ac;③a+b+c>0;④2a+b<0.
其中,正确的结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 此题可利用排除法进行判断,根据二次函数图象的开口方向确定a>0,再根据对称轴在y轴左,可确定a与b同号,然后再根据二次函数与y轴的交点可以确定c<0,进而可以判断出①的正误,然后再根据抛物线与x轴的交点个数可以判断出②的正误,再根据x=1时,结合图象可得到y的正负,进而可以判断出③的正误,由对称轴=-$\frac{b}{2a}$<1,可得出$\frac{b}{2a}$>-1,得出2a+b<0,进而可以判断出④的正误,进而得到答案.
解答 解:∵抛物线开口向下,
∴a<0,
∵对称轴在y轴右侧,
∴a与b异号,
∴b>0,
∵抛物线与y轴交于正半轴,
∴c>0,
∴abc<0,故①正确;
∵抛物线与x轴有两个交点,
∴b2-4ac>0,
∴b2>4ac,故②正确;
当x=1时,y>0,
∴a+b+c>0,故③正确;
∵抛物线的对称轴x=-$\frac{b}{2a}$<1,
∴$\frac{b}{2a}$>-1,
∵a<0,
∴b<-2a,
∴2a+b<0,故④正确;
故选:D.
点评 此题主要考查了二次函数图象与系数的关系,关键是掌握二次函数y=ax2+bx+c(a≠0),
①二次项系数a决定抛物线的开口方向和大小.
当a>0时,抛物线向上开口;当a<0时,抛物线向下开口.
②一次项系数b和二次项系数a共同决定对称轴的位置.
当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)
③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).
④抛物线与x轴交点个数.
△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
10. 如图,某酒店大门的旋转门内部由三块宽为2米,高为3米的玻璃隔板组成,三块玻璃摆放时夹角相同.若入口处两根立柱之间的距离为2米,则两立柱底端中点到中央转轴底端的距离为( )
如图,某酒店大门的旋转门内部由三块宽为2米,高为3米的玻璃隔板组成,三块玻璃摆放时夹角相同.若入口处两根立柱之间的距离为2米,则两立柱底端中点到中央转轴底端的距离为( )
 如图,某酒店大门的旋转门内部由三块宽为2米,高为3米的玻璃隔板组成,三块玻璃摆放时夹角相同.若入口处两根立柱之间的距离为2米,则两立柱底端中点到中央转轴底端的距离为( )
如图,某酒店大门的旋转门内部由三块宽为2米,高为3米的玻璃隔板组成,三块玻璃摆放时夹角相同.若入口处两根立柱之间的距离为2米,则两立柱底端中点到中央转轴底端的距离为( )| A. | $\sqrt{3}$米 | B. | 2米 | C. | 2$\sqrt{2}$米 | D. | 3米 |
14.在期中考试中,七年级一班51名学生的总分是a分,七年级二班49名学生的平均分是b分,则这两个班的平均分是( )
| A. | $\frac{a+49b}{100}$ | B. | $\frac{51a+b}{100}$ | C. | $\frac{a+b}{100}$ | D. | $\frac{51a+49b}{100}$ |
4.下列语句叙述正确的个数是( )
①横坐标与纵坐标互为相反数的点在直线y=-x上;
②点P(2,0)在y轴上;
③若点P的坐标为(a,b),且ab=0,则P点是坐标原点;
④函数y=1-x中y随x的增大而增大.
①横坐标与纵坐标互为相反数的点在直线y=-x上;
②点P(2,0)在y轴上;
③若点P的坐标为(a,b),且ab=0,则P点是坐标原点;
④函数y=1-x中y随x的增大而增大.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.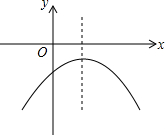 抛物线y=ax2+bx+c的图象如图所示,则( )
抛物线y=ax2+bx+c的图象如图所示,则( )
 抛物线y=ax2+bx+c的图象如图所示,则( )
抛物线y=ax2+bx+c的图象如图所示,则( )| A. | a<0,△<0,b>0 | B. | a<0,△>0,b>0 | C. | a<0,△<0,b<0 | D. | a<0,△>0,b<0 |