题目内容
10．
如图，某酒店大门的旋转门内部由三块宽为2米，高为3米的玻璃隔板组成，三块玻璃摆放时夹角相同．若入口处两根立柱之间的距离为2米，则两立柱底端中点到中央转轴底端的距离为（ ）| A． | $\sqrt{3}$米 | B． | 2米 | C． | 2$\sqrt{2}$米 | D． | 3米 |
分析 由题意可知：中央转轴就是三块玻璃的交点O，三块玻璃在转动中形成以O为圆心，以2米为半径的圆，再根据两根立柱之间的距离为2米，由此画出图形，利用等边三角形的判定与性质，直角三角形的性质解决问题即可，
解答 解：如图，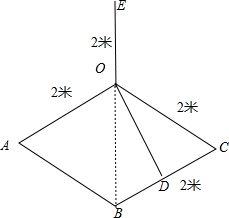
三块玻璃分别为OA、OC、OE，且OA=OC=OE，
且两根立柱BC之间的距离为2米，
连接OB，
则OB=OE，
∵OB=BC=OC，
∴△OBC是等边三角形，
∵D是BC的中点，
∴OD⊥BC，CD=1米，
∴OD=$\sqrt{O{C}^{2}-C{D}^{2}}$=$\sqrt{3}$米．
故选：A．
点评 此题考查解直角三角形，等边三角形的判定与性质，勾股定理的运用，正确理解题意，画出图形，直观解决问题．
练习册系列答案
中考利剑中考试卷汇编系列答案
相关题目
18．
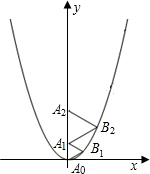二次函数y=$\frac{2}{3}$x2的图象如图所示，点A0位于坐标原点，点 A1，A2在y轴的正半轴上，点B1，B2在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上，若△A0B1A1，△A1B2A2都为等边三角形，则△A1B2A2的边长（ ）
二次函数y=$\frac{2}{3}$x2的图象如图所示，点A0位于坐标原点，点 A1，A2在y轴的正半轴上，点B1，B2在二次函数y=$\frac{2}{3}$x2位于第一象限的图象上，若△A0B1A1，△A1B2A2都为等边三角形，则△A1B2A2的边长（ ）| A． | $\frac{2}{3}$ | B． | $\frac{4}{3}$ | C． | 2 | D． | 3 |
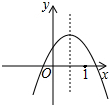已知抛物线y=ax2+bx+c（a≠0）在平面直角坐标系中的位置如图所示，则下列结论：
如图，已知：在△ABC中，∠ABC的平分线与AC边的垂直平分线相交于点N，过点N作ND⊥AB于D，NE⊥BC于E．求证：AD=CE．