题目内容
1.在Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,以C为圆心,$\frac{24}{5}$cm为半径的圆与直线AB相切,切点到点A的距离为$\frac{18}{5}$cm.分析 作CD⊥AB于D,如图,利用勾股定理计算得AB=10,再利用面积法可计算出CD=$\frac{24}{5}$,接着利用勾股定理计算出AD=$\frac{18}{5}$,然后根据直线与圆相切的定义可得以C为圆心,CD的长为半径的圆与直线AB相切于D点,即切点到点A的距离为$\frac{18}{5}$cm.
解答 解:作CD⊥AB于D,如图,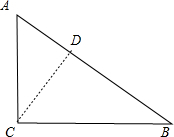 ∠C=90°,AC=6cm,BC=8cm,
∠C=90°,AC=6cm,BC=8cm,
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵$\frac{1}{2}$CD•AB=$\frac{1}{2}$AC•BC,
∴CD=$\frac{6×8}{10}$=$\frac{24}{5}$,
在Rt△ACD中,AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{{6}^{2}-(\frac{24}{5})^{2}}$=$\frac{18}{5}$,
∴以C为圆心,$\frac{24}{5}$cm为半径的圆与直线AB相切于D点,
∴切点到点A的距离为$\frac{18}{5}$cm.
故答案为$\frac{24}{5}$,$\frac{18}{5}$.
点评 本题考查了直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,则直线l和⊙O相交?d<r;直线l和⊙O相切?d=r;直线l和⊙O相离?d>r.也考查了勾股定理.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
9.小虎的身高为1.6米,他的影长为2米,同一时刻他测得电线杆的影长为18米,则此电线杆的高度为( )
| A. | 20米 | B. | 14.4米 | C. | 16.4米 | D. | 15.4米 |
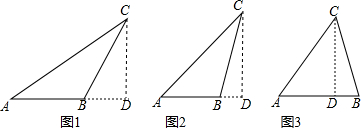
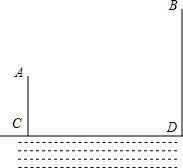 如图,A,B两个村子在一条河的同侧,A,B两村到河岸的距离分别为AC=1km,BD=3km,其中CD=3km.现在要在河岸CD上建一个水厂,向A,B两个村庄输送自来水,请你在CD上选择水厂的位置O,使铺设的水管总长度最小?
如图,A,B两个村子在一条河的同侧,A,B两村到河岸的距离分别为AC=1km,BD=3km,其中CD=3km.现在要在河岸CD上建一个水厂,向A,B两个村庄输送自来水,请你在CD上选择水厂的位置O,使铺设的水管总长度最小?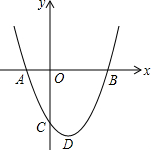 如图,抛物线y=x2+bx+c交x轴于点A(-1,0)和点B(m,0),交y轴于点C,抛物线的顶点为D,m>1.
如图,抛物线y=x2+bx+c交x轴于点A(-1,0)和点B(m,0),交y轴于点C,抛物线的顶点为D,m>1.
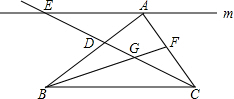 如图,点G是△ABC的重心,直线m过点A且与BC平行,若射线CG分别交直线m及线段AB于E、D两点,则S△AED:S四边形ADGF=3:2.
如图,点G是△ABC的重心,直线m过点A且与BC平行,若射线CG分别交直线m及线段AB于E、D两点,则S△AED:S四边形ADGF=3:2.