题目内容
13.观察下列各式:$\sqrt{3+\frac{3}{2}}$=3$\sqrt{\frac{1}{2}}$,$\sqrt{4+\frac{4}{3}}$=4$\sqrt{\frac{1}{3}}$,$\sqrt{5+\frac{5}{4}}$=5$\sqrt{\frac{1}{4}}$,…,那么如果用字母n(n≥2的整数)表示上面的规律应该是$\sqrt{n+1+\frac{n+1}{n}}$=(n+1)$\sqrt{\frac{1}{n}}$.分析 根据第一个等式是$\sqrt{2+1+\frac{2+1}{2}}$=(2+1)$\sqrt{\frac{1}{2}}$,第二个等式是$\sqrt{3+1+\frac{3+1}{3}}$=(3+1)$\sqrt{\frac{1}{3}}$,总结规律,得到答案.
解答 解:第一个等式是$\sqrt{2+1+\frac{2+1}{2}}$=(2+1)$\sqrt{\frac{1}{2}}$,
第二个等式是$\sqrt{3+1+\frac{3+1}{3}}$=(3+1)$\sqrt{\frac{1}{3}}$,
则规律为:$\sqrt{n+1+\frac{n+1}{n}}$=(n+1)$\sqrt{\frac{1}{n}}$.
点评 本题考查的是二次根式的性质与化简,从已知式子中找出规律是解题的关键,注意分子、分母之间的关系.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
18.把a$\sqrt{-\frac{1}{a}}$根号外的因式移到根号内,化简的结果是( )
| A. | $\sqrt{a}$ | B. | $\sqrt{-a}$ | C. | -$\sqrt{a}$ | D. | -$\sqrt{-a}$ |
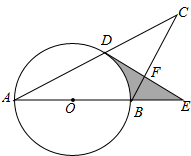 如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过点D作⊙O的切线DE,分别交BC,AB的延长线于点F,E.
如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过点D作⊙O的切线DE,分别交BC,AB的延长线于点F,E.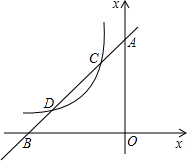 如图,直线y1=x+m,分别与x轴、y轴交于点A、B,与双曲线y2=(x<0)的图象相交于点C、D,其中(-1,2).
如图,直线y1=x+m,分别与x轴、y轴交于点A、B,与双曲线y2=(x<0)的图象相交于点C、D,其中(-1,2).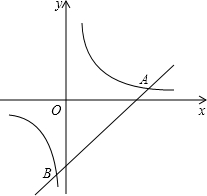 如图,已知一次函数y1=x-6与反比例函数y2=$\frac{7}{x}$的图象交于A、B两点.
如图,已知一次函数y1=x-6与反比例函数y2=$\frac{7}{x}$的图象交于A、B两点.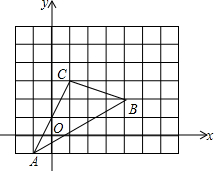 如图,△ABC在直角坐标系中
如图,△ABC在直角坐标系中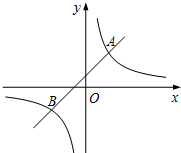 如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{6}{x}$的图象交于A(m,3),B(-3,n)两点.
如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{6}{x}$的图象交于A(m,3),B(-3,n)两点.