题目内容
19.已知点A(a,b),B(a,c),且a≠0,b≠c,那么直线AB与坐标轴有什么位置关系?分析 根据点A(a,b),B(a,c),且a≠0,b≠c,可知点A、B的横坐标相等,纵坐标不相等,从而可以得到直线AB与坐标轴的位置关系.
解答 解:∵点A(a,b),B(a,c),且a≠0,b≠c,
∴点A、B的横坐标相等,纵坐标不相等,点A、B所在的直线不与y轴重合.
∴直线AB与y轴平行.
即直线AB与坐标轴的位置关系是:直线AB与y轴平行.
点评 本题考查坐标与图形的性质,解题的关键是明确两个点的横坐标相等,则这两个点所在的直线与y轴平行.

练习册系列答案
相关题目
10.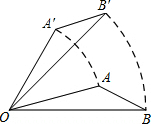 如图,将△AOB绕点O按逆时针旋转45°后得到△A′OB′,若∠AOB=15°,则∠A′OB的度数是( )
如图,将△AOB绕点O按逆时针旋转45°后得到△A′OB′,若∠AOB=15°,则∠A′OB的度数是( )
 如图,将△AOB绕点O按逆时针旋转45°后得到△A′OB′,若∠AOB=15°,则∠A′OB的度数是( )
如图,将△AOB绕点O按逆时针旋转45°后得到△A′OB′,若∠AOB=15°,则∠A′OB的度数是( )| A. | 25° | B. | 30° | C. | 35 | D. | 60° |
11.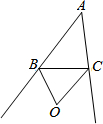 如图,点O是△ABC的两外角平分线的交点,下列结论:①OB=OC;②点O到AB、AC的距离相等;③点O到△ABC的三边的距离相等;④点O在∠A的平分线上.其中结论正确的个数是( )
如图,点O是△ABC的两外角平分线的交点,下列结论:①OB=OC;②点O到AB、AC的距离相等;③点O到△ABC的三边的距离相等;④点O在∠A的平分线上.其中结论正确的个数是( )
 如图,点O是△ABC的两外角平分线的交点,下列结论:①OB=OC;②点O到AB、AC的距离相等;③点O到△ABC的三边的距离相等;④点O在∠A的平分线上.其中结论正确的个数是( )
如图,点O是△ABC的两外角平分线的交点,下列结论:①OB=OC;②点O到AB、AC的距离相等;③点O到△ABC的三边的距离相等;④点O在∠A的平分线上.其中结论正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
9.关于x的方程abx2-(a2+b2)x+ab=0(ab≠0)的根是( )
| A. | x1=$\frac{2b}{a}$,x2=$\frac{2a}{b}$ | B. | x1=$\frac{b}{a}$,x2=$\frac{a}{b}$ | ||
| C. | x1=$\frac{{a}^{2}+{b}^{2}}{ab}$,x2=0 | D. | 以上都不正确 |
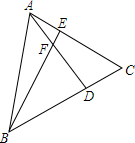 如图,在等边三角形ABC中,点E、D分别从A、C出发,沿AC,CB方向以相同的速度在线段AC,CB上运动,AD、BE相交于F点.
如图,在等边三角形ABC中,点E、D分别从A、C出发,沿AC,CB方向以相同的速度在线段AC,CB上运动,AD、BE相交于F点.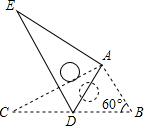 如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AC=$\sqrt{3}$,∠B=60°,则CD的长为1.
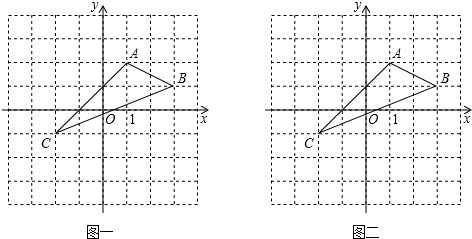
如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上,若AC=$\sqrt{3}$,∠B=60°,则CD的长为1.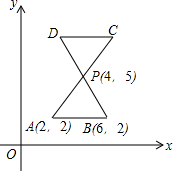 如图,AC与BD交于P点,PA=PB=PC=PD,已知△PAB的三点坐标为A(2,2),B(6,2),P(4,5).
如图,AC与BD交于P点,PA=PB=PC=PD,已知△PAB的三点坐标为A(2,2),B(6,2),P(4,5).