题目内容
11.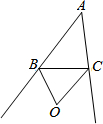 如图,点O是△ABC的两外角平分线的交点,下列结论:①OB=OC;②点O到AB、AC的距离相等;③点O到△ABC的三边的距离相等;④点O在∠A的平分线上.其中结论正确的个数是( )
如图,点O是△ABC的两外角平分线的交点,下列结论:①OB=OC;②点O到AB、AC的距离相等;③点O到△ABC的三边的距离相等;④点O在∠A的平分线上.其中结论正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 过点O作OE⊥AB于E,作OF⊥BC于F,作OG⊥AC于G,根据角平分线上的点到角的两边的距离相等可得OE=OF=OG,再根据到角的两边距离相等的点在角的平分线上解答.
解答  解:如图,过点O作OE⊥AB于E,作OF⊥BC于F,作OG⊥AC于G,
解:如图,过点O作OE⊥AB于E,作OF⊥BC于F,作OG⊥AC于G,
∵点O是△ABC的两外角平分线的交点,
∴OE=OG,OF=OG,
∴OE=OF=OG,
∴点O在∠B的平分线上,故②③④正确,
只有点G是AC的中点时,BO=CO,故①错误,
综上所述,说法正确的是②③④.
故选C.
点评 本题考查了角平分线上的点到角的两边的距离相等的性质,到角的两边距离相等的点在角的平分线上,熟记性质并作出辅助线是解题的关键

练习册系列答案
相关题目
6.在直角坐标系中,一条直线平行y轴,且到y轴的距离为2,点P(x,y)在该直线上,那么下列说法正确的是( )
| A. | x=2 | B. | y=2 | C. | x=±2 | D. | y=±2 |
20.下列方程是二元一次方程的是( )
| A. | 3x+2y=6 | B. | xy-2x-3=0 | C. | $\frac{x}{2}+\frac{5}{3}=\frac{7}{4}x$ | D. | $\frac{2}{x}+3y=2\frac{1}{3}$ |
1.一元二次方程3x2-x=2的二次项系数、一次项系数和常数项分别是( )
| A. | 3、-1、-2 | B. | 3、-1、2 | C. | -3、1、-2 | D. | -3、-1、2 |
 如图所示,在△ABC中,AB=AC,在AB上取一点E,在AC延长线上取一点F,使BE=CF,EF交BC于G.求证:EG=FG.
如图所示,在△ABC中,AB=AC,在AB上取一点E,在AC延长线上取一点F,使BE=CF,EF交BC于G.求证:EG=FG.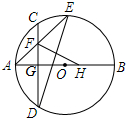 如图,AB是⊙O的直径,点A为$\widehat{CD}$的中点,点F是CG的中点,AF的延长线交⊙O于点E,点H是BG的中点,tanE=$\frac{1}{2}$.
如图,AB是⊙O的直径,点A为$\widehat{CD}$的中点,点F是CG的中点,AF的延长线交⊙O于点E,点H是BG的中点,tanE=$\frac{1}{2}$.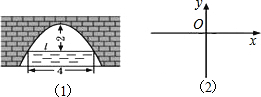 如图(1)是一个横截面为抛物线形拱桥,当拱顶高水面2m时,水面宽4m.如图(2)所示建立在平面直角坐标系中,则抛物线的解析式是y=-$\frac{1}{2}$x2.
如图(1)是一个横截面为抛物线形拱桥,当拱顶高水面2m时,水面宽4m.如图(2)所示建立在平面直角坐标系中,则抛物线的解析式是y=-$\frac{1}{2}$x2.