题目内容
6.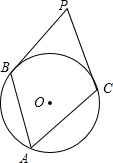 如图,圆周角∠BAC=55°,分别过B、C两点作⊙O的切线相交于P,则∠BPC为( )
如图,圆周角∠BAC=55°,分别过B、C两点作⊙O的切线相交于P,则∠BPC为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
分析 首先连接OB,OC,由PB,PC是⊙O的切线,利用切线的性质,即可求得∠PBO=∠PCO=90°,又由圆周角定理可得:∠BOC=2∠BAC,继而求得∠BPC的度数
解答  解:连接OB,OC,
解:连接OB,OC,
∵PB,PC是⊙O的切线,
∴OB⊥PB,OC⊥PC,
∴∠PBO=∠PCO=90°,
∵∠BOC=2∠BAC=2×55°=110°,
∴∠BPC=360°-∠PBO-∠BOC-∠PCO=360°-90°-110°-90°=70°.
故答案为:70.
点评 此题考查了切线的性质、圆周角定理以及四边形的内角和定理.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
16.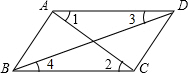 如图,在下列条件中,能判定AB∥CD的有( )
如图,在下列条件中,能判定AB∥CD的有( )
 如图,在下列条件中,能判定AB∥CD的有( )
如图,在下列条件中,能判定AB∥CD的有( )| A. | ∠BAD=∠BCD | B. | ∠ABD=∠BDC | C. | ∠ABC+∠BAD=180° | D. | ∠1=∠2 |
14.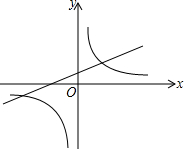 如图,是函数y=kx+1与y=$\frac{k}{x}$(k≠0)在同一直角坐标系中的大致图象,则下列结论正确的是( )
如图,是函数y=kx+1与y=$\frac{k}{x}$(k≠0)在同一直角坐标系中的大致图象,则下列结论正确的是( )
 如图,是函数y=kx+1与y=$\frac{k}{x}$(k≠0)在同一直角坐标系中的大致图象,则下列结论正确的是( )
如图,是函数y=kx+1与y=$\frac{k}{x}$(k≠0)在同一直角坐标系中的大致图象,则下列结论正确的是( )| A. | k<1 | B. | k>0 | C. | k<0 | D. | k>1 |
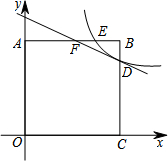 如图,正方形AOCB的边长为4,反比例函数y=$\frac{k}{x}$的图象过点E(3,4),与线段BC交于点D,直线y=-$\frac{1}{2}$x+b过点D,与线段AB相交于点F,连接OF,OE,请你探究∠AOF与∠EOC的数量关系,并证明.
如图,正方形AOCB的边长为4,反比例函数y=$\frac{k}{x}$的图象过点E(3,4),与线段BC交于点D,直线y=-$\frac{1}{2}$x+b过点D,与线段AB相交于点F,连接OF,OE,请你探究∠AOF与∠EOC的数量关系,并证明.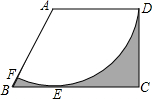 如图,在直角梯形ABCD中,AD∥BC,DC⊥BC,以点A为圆心,AD为半径的圆与BC相切于点E,与AB相交于点F,若AD=$\sqrt{3}$,BE=1,则图中阴影部分的面积为3$+\frac{\sqrt{3}}{2}-π$.
如图,在直角梯形ABCD中,AD∥BC,DC⊥BC,以点A为圆心,AD为半径的圆与BC相切于点E,与AB相交于点F,若AD=$\sqrt{3}$,BE=1,则图中阴影部分的面积为3$+\frac{\sqrt{3}}{2}-π$.