题目内容
9.计算(1)($\frac{2}{3}$-$\frac{1}{2}$)×30÷(-$\frac{1}{5}$)
(2)-42+3×(-2)3×($\frac{1}{3}$-1)÷(-1$\frac{1}{3}$)
(3)-22÷(-4)3+|0.8-1|×${(2\frac{1}{2})}^{2}$
(4)-13×$\frac{2}{3}$-0.34×$\frac{2}{7}$+$\frac{1}{3}$×(-13)-$\frac{5}{7}$×0.34(用简便方法计算)
分析 (1)原式先计算括号中的减法运算,再计算乘除运算即可得到结果;
(2)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果;
(3)原式先计算乘方及绝对值运算,再计算乘除运算,最后算加减运算即可得到结果;
(4)原式结合后,逆用乘法分配律计算即可得到结果.
解答 解:(1)原式=$\frac{1}{6}$×30×(-5)=-25;
(2)原式=-16-24×(-$\frac{2}{3}$)×(-$\frac{3}{4}$)=-16-12=-28;
(3)原式=-4÷(-64)+0.2×$\frac{25}{4}$=$\frac{1}{16}$+$\frac{5}{4}$=$\frac{21}{16}$;
(4)原式=(-13)×($\frac{2}{3}$+$\frac{1}{3}$)-0.34×($\frac{2}{7}$+$\frac{5}{7}$)=-13.34.
点评 此题考查了有理数的混合运算,以及乘法分配律,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
14.已知关于x的一元二次方程(m-1)x2+x+m2+2m-3=0的一个根为0,则m的值为( )
| A. | m=-3 | B. | m=1 | C. | m=1或m=-3 | D. | m≠1 |
18.下列计算中,正确的是( )
| A. | (-xy)3=-xy3 | B. | (2x2y)2=2x4y2 | C. | ($\frac{2}{3}$x2y)2=$\frac{3}{4}$x4y2 | D. | ($\frac{1}{3}$xy2)3=$\frac{1}{27}$x3y6 |
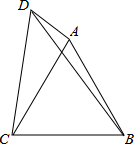 如图,在四边形ABCD中,△ABC是等边三角形,∠ADC=∠ABC,若AD=3,BC=7,则线段BD的长为$\sqrt{97}$.
如图,在四边形ABCD中,△ABC是等边三角形,∠ADC=∠ABC,若AD=3,BC=7,则线段BD的长为$\sqrt{97}$.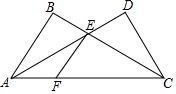 如图,已知AB⊥BC,EF⊥BC,CD⊥AD.
如图,已知AB⊥BC,EF⊥BC,CD⊥AD.