题目内容
17.某人沿斜坡坡度i=1:2的斜坡向上前进了6米,则他上升的高度为( )| A. | 3米 | B. | $\frac{6\sqrt{5}}{5}$米 | C. | 2$\sqrt{3}$米 | D. | $\frac{12\sqrt{5}}{5}$米 |
分析 由坡度定义可得位置升高的高度即为坡角所对的直角边.根据题意可得tan∠A=$\frac{1}{2}$,AB=10m,可解出直角边BC,即得到位置升高的高度.
解答 解:由题意得,BC:AC=1:2.
∴BC:AB=1:$\sqrt{5}$.
∵AB=6m,
∴BC=$\frac{6\sqrt{5}}{5}$m.
故选B.
点评 本题主要考查坡度的定义和解直角三角形的应用,注意画出示意图会使问题具体化.

练习册系列答案
相关题目
9.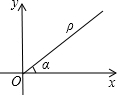 如图,在平面直角坐标系中,设点P到原点O的距离为ρ,OP与x轴正方向的交角为a,则用[ρ,a]表示点P的极坐标,例如:点P的坐标为(1,1),则其极坐标为[$\sqrt{2}$,45°].若点Q的极坐标为[4,120°],则点Q的平面坐标为( )
如图,在平面直角坐标系中,设点P到原点O的距离为ρ,OP与x轴正方向的交角为a,则用[ρ,a]表示点P的极坐标,例如:点P的坐标为(1,1),则其极坐标为[$\sqrt{2}$,45°].若点Q的极坐标为[4,120°],则点Q的平面坐标为( )
 如图,在平面直角坐标系中,设点P到原点O的距离为ρ,OP与x轴正方向的交角为a,则用[ρ,a]表示点P的极坐标,例如:点P的坐标为(1,1),则其极坐标为[$\sqrt{2}$,45°].若点Q的极坐标为[4,120°],则点Q的平面坐标为( )
如图,在平面直角坐标系中,设点P到原点O的距离为ρ,OP与x轴正方向的交角为a,则用[ρ,a]表示点P的极坐标,例如:点P的坐标为(1,1),则其极坐标为[$\sqrt{2}$,45°].若点Q的极坐标为[4,120°],则点Q的平面坐标为( )| A. | (-2,2$\sqrt{3}$) | B. | (2,-2$\sqrt{3}$) | C. | (-2$\sqrt{3}$,-2) | D. | (-4,-4$\sqrt{3}$) |
6.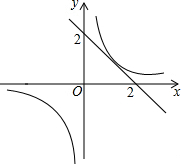 如图已知一次函数y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点,则b的取值范围是( )
如图已知一次函数y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点,则b的取值范围是( )
 如图已知一次函数y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点,则b的取值范围是( )
如图已知一次函数y=-x+b与反比例函数y=$\frac{1}{x}$的图象有2个公共点,则b的取值范围是( )| A. | b>2 | B. | -2<b<2 | C. | b>2或b<-2 | D. | b<-2 |


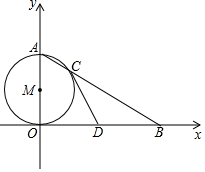 如图,OA是⊙M的直径,点B在x轴上,连接AB交⊙M于点C.
如图,OA是⊙M的直径,点B在x轴上,连接AB交⊙M于点C.