题目内容
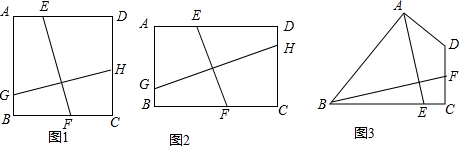
17.【探究】已知,点E,F,G,H分别在四边形ABCD的四条边上,且EF⊥GH.
(1)如图1,若四边形ABCD为正方形,EF=a,则GH=a;
(2)如图2,若四边形ABCD为矩形,AB=a,BC=b,求$\frac{EF}{GH}$的值.
【拓展】
如图3,四边形ABCD中,点E,F分别在BC,CD上,且AE⊥BF,若∠BCD=90°,AB=BC=20,AD=CD=10,求$\frac{AE}{BF}$的值.
分析 (1)先判断出∠EFN=∠GHM,进而得出△MGH≌△NEF,即可得出结论;
(2)同(1)的方法判断出∠MGH=∠NEF,从而得出△FEN∽△HGM,即可得出结论;
(3)先判断出△ABD≌△CBD,再用勾股定理即可求出BG,即可得出结论.
解答 解:(1)如图1, 过点G作GM⊥CD于M,过点E作EN⊥BC于点N,
过点G作GM⊥CD于M,过点E作EN⊥BC于点N,
∴∠GMH=∠ENF=90°,
∵四边形ABCD是正方形,
∴∠B=90°,AB=BC,
∴GM=EN,
∵EF⊥GH,∠B=90°,
∴∠BGH+∠BFE=180°,
∵∠BGM=90°,
∴∠MGH+∠EFN=90°,
∵EF⊥GH,∠C=90°,
∴∠EFN=∠GHM,
∴∠MGH=∠NEF,
在△MGH和△NEF中,$\left\{\begin{array}{l}{∠MGE=∠NEF}\\{GM=EN}\\{∠GMH=∠ENF}\end{array}\right.$,
∴△MGH≌△NEF,
∴GH=EF=a,
故答案为a;
(2)如图2, 过点G作GM⊥CD于M,过点E作EN⊥BC于点N,
过点G作GM⊥CD于M,过点E作EN⊥BC于点N,
∴E
N=AB,GM=BC,
同(1)的得,∠MGH=∠NEF,
∵∠GMH=∠ENF,
∴△FEN∽△HGM,
∴$\frac{EF}{GH}=\frac{EN}{GM}$,
∴$\frac{EF}{GH}=\frac{AB}{BC}=\frac{a}{b}$;
(3)如图3, 过点A作GH∥BC,过点B作BG⊥GH于点G,延长CD交GH于点H,连接BD,
过点A作GH∥BC,过点B作BG⊥GH于点G,延长CD交GH于点H,连接BD,
∴四边形BCHG是矩形,
在△ABD和△CBD中,$\left\{\begin{array}{l}{AB=CB}\\{AD=CD}\\{BD=BD}\end{array}\right.$,
∴△ABD≌△CBD,
∴∠BAD=∠C=90°,
∴△ADH∽△BAG,
∴$\frac{DH}{AG}=\frac{AD}{AB}=\frac{1}{2}$,
设DH=x,
∴AG=2x,BG=x+10,
在Rt△ABG中,由勾股定理得,(2x)2+(x+10)2=400,
∴x=-10(舍)或x=6,
由(2)知,$\frac{AE}{BF}=\frac{BG}{BC}=\frac{4}{5}$.
点评 此题是相似形综合题,主要考查了正方形的性质,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理.解(1)的关键是构造全等三角形,解(2)的关键是判断出△FEN∽△HGM,解(3)的关键是求出BG是一道很好的中考常考题.

 期末集结号系列答案
期末集结号系列答案| A. |  | B. |  | C. |  | D. |  |
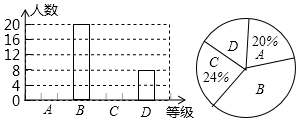 某校九年级一次模拟考试后,数学考试为了了解学生的学习情况,在全校1000名九年级学生中,随机抽取了50名学生的数学成绩进行统计分析,并绘制了如下统计表和统计图(部分信息未给全).
某校九年级一次模拟考试后,数学考试为了了解学生的学习情况,在全校1000名九年级学生中,随机抽取了50名学生的数学成绩进行统计分析,并绘制了如下统计表和统计图(部分信息未给全). | 成绩/分 | 111~120 | 101~110 | 91~100 | 90及90以下 |
| 等级 | A | B | C | D |
| 学生人数 | m | 20 | n | 8 |
(1)补全条形统计图,并求出扇形统计图中,表示成绩为B等级的扇形所对的圆心角的度数;
(2)被调查学生在这次模拟考试中,数学成绩的中位数落在B等级.
(3)请估计该校九年级学生在这次模拟考试中,数学成绩在B等级以上(含B等级)的学生可达多少名?
| 销售量p(件) | p=50-x |
| 销售单价q(元/件) | 当1≤x≤20时,q=30+$\frac{1}{2}$x 当21≤x≤40时,q=20+$\frac{525}{x}$ |
(2)这40天中该加盟店第几天获得的利润最大?最大利润是多少?
(3)在实际销售的前20天中,公司为鼓励加盟店接收大学生参加实践活动决定每销售一件商品就发给该加盟店m(m≥2)元奖励.通过该加盟店的销售记录发现,前10天中,每天获得奖励后的利润随时间x(天)的增大而增大,求m的取值范围.
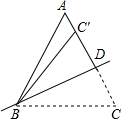 如图,在△ABC中,AB=AC=10,将△ABC沿直线BD翻折,使点C落在AC边上的点C′处,若AC′=2,则折痕BD的长8.
如图,在△ABC中,AB=AC=10,将△ABC沿直线BD翻折,使点C落在AC边上的点C′处,若AC′=2,则折痕BD的长8.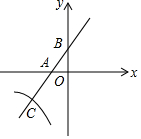 如图,已知一次函数${y}_{1}=\frac{4}{3}x+4$的图象分别交x轴于A、B两点,交反比例函数y2=$\frac{a}{x}$(x<0)的图象于第三象限的C点,且AB=AC.
如图,已知一次函数${y}_{1}=\frac{4}{3}x+4$的图象分别交x轴于A、B两点,交反比例函数y2=$\frac{a}{x}$(x<0)的图象于第三象限的C点,且AB=AC.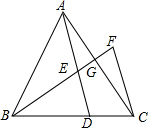 如图,已知△ABC中,D、G分别是边BC、AC上的点,连AD、BC相交于点E,BE=BD.过点C作AD的平行线与BG的延长线于点F,$\frac{CD}{BD}$=$\frac{1}{2}$,$\frac{DE}{EA}$=$\frac{2}{3}$.
如图,已知△ABC中,D、G分别是边BC、AC上的点,连AD、BC相交于点E,BE=BD.过点C作AD的平行线与BG的延长线于点F,$\frac{CD}{BD}$=$\frac{1}{2}$,$\frac{DE}{EA}$=$\frac{2}{3}$.