题目内容
15.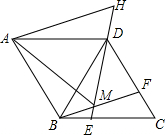 如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形④S四边形ABMD=$\frac{\sqrt{3}}{4}$AM2.
如图,在菱形ABCD中,AB=BD,点E、F分别在BC、CD上,且BE=CF,连接BF、DE交于点M,延长ED到H使DH=BM,连接AM,AH,则以下四个结论:①△BDF≌△DCE;②∠BMD=120°;③△AMH是等边三角形④S四边形ABMD=$\frac{\sqrt{3}}{4}$AM2.其中正确结论的是①②③④.
分析 先证明△ABD是等边三角形,再根据菱形的性质可得∠BDF=∠C=60°,再求出DF=CE,然后利用“边角边”即可证明△BDF≌△DCE,从而判定①正确;
根据全等三角形对应角相等可得∠DBF=∠EDC,由三角形的外角性质求出∠DMF=∠BDC=60°,再求出∠BMD=120°,从而判定②正确;
根据三角形的外角性质和平行线的性质求出∠ABM=∠ADH,由SAS证明△ABM≌△ADH,根据全等三角形的性质得出AH=AM,∠BAM=∠DAH,然后求出∠MAH=∠BAD=60°,从而判定出△AMH是等边三角形,得出③正确;
根据全等三角形的面积相等可得△AMH的面积等于四边形ABMD的面积,然后判定出④正确.
解答 解:在菱形ABCD中,
∵AB=BD,
∴AB=BD=AD,
∴△ABD是等边三角形,
∴根据菱形的性质可得∠BDF=∠C=60°,
∵BE=CF,
∴BC-BE=CD-CF,
即CE=DF,
在△BDF和△DCE中,$\left\{\begin{array}{l}{CE=DF}&{\;}\\{∠BDF=∠C=60°}&{\;}\\{BD=CD}&{\;}\end{array}\right.$,
∴△BDF≌△DCE(SAS),故①正确;
∴∠DBF=∠EDC,
∵∠DMF=∠DBF+∠BDE=∠EDC+∠BDE=∠BDC=60°,
∴∠BMD=180°-∠DMF=180°-60°=120°,故②正确;
∵∠DEB=∠EDC+∠C=∠EDC+60°,∠ABM=∠ABD+∠DBF=∠DBF+60°,
∴∠DEB=∠ABM,
又∵AD∥BC,
∴∠ADH=∠DEB,
∴∠ADH=∠ABM,
在△ABM和△ADH中,$\left\{\begin{array}{l}{AB=AD}&{\;}\\{∠ADH=∠ABM}&{\;}\\{DH=BM}&{\;}\end{array}\right.$,
∴△ABM≌△ADH(SAS),
∴AH=AM,∠BAM=∠DAH,
∴∠MAH=∠MAD+∠DAH=∠MAD+∠BAM=∠BAD=60°,
∴△AMH是等边三角形,故③正确;
∵△ABM≌△ADH,
∴△AMH的面积等于四边形ABMD的面积,
又∵△AMH的面积=$\frac{1}{2}$AM•$\frac{\sqrt{3}}{2}$AM=$\frac{\sqrt{3}}{4}$AM2,
∴S四边形ABMD=$\frac{\sqrt{3}}{4}$AM2,故④正确,
综上所述,正确的是①②③④.
故答案为:①②③④.
点评 本题是四边形综合题目,考查了菱形的性质,全等三角形的判定与性质,等边三角形的判定与性质,题目较为复杂,特别是图形的识别有难度,从图形中准确确定出全等三角形并找出全等的条件是解题的关键.

 如图,在?ABCD中,∠ABC=60°,点E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,CF=$\sqrt{5}$.
如图,在?ABCD中,∠ABC=60°,点E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,CF=$\sqrt{5}$.(1)求证:四边形ABDE是平行四边形;
(2)连接DF,求DF的长.
| 种类 | 单价 |
| 米饭 | 0.5元/份 |
| A类套餐菜 | 3.5元/份 |
| B类套餐菜 | 2.5元/份 |
 如图,矩形ABCD中,AB=2,点E在AD边上,以E为圆心EA长为半径的⊙E与BC相切,交CD于点F,连接EF.若扇形EAF的面积为$\frac{4}{3}$π,则BC的长是3.
如图,矩形ABCD中,AB=2,点E在AD边上,以E为圆心EA长为半径的⊙E与BC相切,交CD于点F,连接EF.若扇形EAF的面积为$\frac{4}{3}$π,则BC的长是3. 绿色出行是对环境影响最小的出行方式,“共享单车”已成为北京的一道靓丽的风景线.某社会实践活动小组为了了解“共享单车”的使用情况,对本校教师在3月6日至3月10日使用单车的情况进行了问卷调查,以下是根据调查结果绘制的统计图的一部分:
绿色出行是对环境影响最小的出行方式,“共享单车”已成为北京的一道靓丽的风景线.某社会实践活动小组为了了解“共享单车”的使用情况,对本校教师在3月6日至3月10日使用单车的情况进行了问卷调查,以下是根据调查结果绘制的统计图的一部分: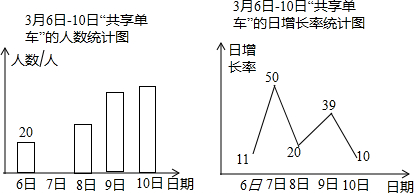
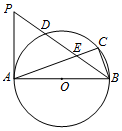 如图,AB是⊙O的直径,BC为弦,D为$\widehat{AC}$的中点,AC,BD相交于E点,过点A作⊙O的切线交BD的延长线于P点.
如图,AB是⊙O的直径,BC为弦,D为$\widehat{AC}$的中点,AC,BD相交于E点,过点A作⊙O的切线交BD的延长线于P点. 如图,抛物线y=ax2+bx+c与x轴交于A(-1,0),B(4,0)与y轴交于点C(0,2),抛物线的对称轴交x轴于点D.
如图,抛物线y=ax2+bx+c与x轴交于A(-1,0),B(4,0)与y轴交于点C(0,2),抛物线的对称轴交x轴于点D. 如图,四边形ABCD中,对角线AC、BD交于点O,且AC⊥BD,AC=BD,SABCD=8cm2,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长等于8cm.
如图,四边形ABCD中,对角线AC、BD交于点O,且AC⊥BD,AC=BD,SABCD=8cm2,E、F、G、H分别是AB、BC、CD、DA的中点,则四边形EFGH的周长等于8cm.