题目内容
13. 如图,BD为?ABCD的对角线,按要求完成下列各题.
如图,BD为?ABCD的对角线,按要求完成下列各题.(1)用直尺和圆规作出对角线BD的垂直平分线交AD于点E,交BC于点F,垂足为O.(保留作图痕迹,不要求写作法)
(2)在(1)的基础上,连接BE和DF.求证:四边形BFDE是菱形.
分析 (1)根据线段垂直平分线的性质画出图形即可;
(2)先根据题意得出△DOE≌△BOF (ASA),故可得出EO=FO,即四边形BFDE 是平行四边形,根据EF⊥BD即可得出结论.
解答  解:(1)如图,E、F即为所求;
解:(1)如图,E、F即为所求;
(2)证明:在□ABCD中,
∵AD∥BC,
∴∠ADB=∠CBD.
又∵EF垂直平分BD,
∴BO=DO,∠EOD=∠FOB=90°,
在△DOE与△BOF中,
∵$\left\{\begin{array}{l}{∠ADB=∠CBD}\\{BO=DO}\\{∠EOD=∠FOB}\end{array}\right.$,
∴△DOE≌△BOF (ASA),
∴EO=FO,
∴四边形BFDE 是平行四边形,
又∵EF⊥BD,
∴□BFDE为菱形.
点评 本题考查的是作图-基本作图,熟知线段垂直平分线的作法是解答此题的关键.

练习册系列答案
相关题目
1.甲、乙两个仓库向A、B两地运送水泥,已知甲库可调出100吨水泥,乙库可调出80吨水泥,A地需70吨,B地需110吨水泥,两库到A,B两地的路程和费用如下表:(表中运费“元/吨•千米”表示每吨水泥运送1千米所需要人民币).
设甲库运往A地水泥x吨,总运费W元.
(1)写出w关于x的函数关系式,并求x为何值时总运费最小?
(2)如果要求运送的水泥数是10吨的整数倍,且运费不能超过38000元,则总共有几种运送方案?
| 路程(千米) | 运费(元/吨•千米) | |||
| 甲库 | 乙库 | 甲库 | 乙库 | |
| A地 | 20 | 15 | 12 | 12 |
| B地 | 25 | 20 | 10 | 8 |
(1)写出w关于x的函数关系式,并求x为何值时总运费最小?
(2)如果要求运送的水泥数是10吨的整数倍,且运费不能超过38000元,则总共有几种运送方案?
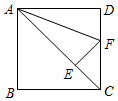 如图,已知E是正方形ABCD对角线AC上的一点,AE=AD,过点E作AC的垂线,交边CD于点F,∠FAD=22.5度.
如图,已知E是正方形ABCD对角线AC上的一点,AE=AD,过点E作AC的垂线,交边CD于点F,∠FAD=22.5度.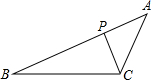 如图,在△ABC中,P是AB边上的点,请补充一个条件,使△ACP∽△ABC,这个条件可以是:∠ACP=∠B(或$\frac{AP}{AC}$=$\frac{AC}{AB}$)(写出一个即可).
如图,在△ABC中,P是AB边上的点,请补充一个条件,使△ACP∽△ABC,这个条件可以是:∠ACP=∠B(或$\frac{AP}{AC}$=$\frac{AC}{AB}$)(写出一个即可).