题目内容
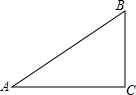 如图,已知Rt△ABC,∠C为直角,请你用尺规,按下列要求作图和计算(不必写画法,但保留作图痕迹)
如图,已知Rt△ABC,∠C为直角,请你用尺规,按下列要求作图和计算(不必写画法,但保留作图痕迹)(1)以AC为一边作等边△ACD;
(2)若设∠A=30°,BC=6,求BD的长.(简单写出解答过程即可)
考点:作图—复杂作图,角平分线的性质,勾股定理
专题:
分析:(1)分别以A、C为圆心,以AC长为半径画弧,相交于点D,连接AD、CD则△ACD即为所求作的等边三角形;
(2)根据30°角所对的直角边等于斜边的一半求出AB的长度,再利用勾股定理求出AC的长度,然后分两种情况:①点D在AC的下方时,作DE⊥BC交BC的延长线于点E,求出DE、CE的长度,然后求出BE的长度,再利用勾股定理列式计算即可得解:;②点D在AC的上方时,求出∠BAD=30°,根据等边三角形的性质可得AB⊥CD,再根据对称性可得△ABD与△ABC关于AB成轴对称,根据轴对称的性质可得BD=BC.
(2)根据30°角所对的直角边等于斜边的一半求出AB的长度,再利用勾股定理求出AC的长度,然后分两种情况:①点D在AC的下方时,作DE⊥BC交BC的延长线于点E,求出DE、CE的长度,然后求出BE的长度,再利用勾股定理列式计算即可得解:;②点D在AC的上方时,求出∠BAD=30°,根据等边三角形的性质可得AB⊥CD,再根据对称性可得△ABD与△ABC关于AB成轴对称,根据轴对称的性质可得BD=BC.
解答:解:(1)如图所示,△ACD为所求作的等边三角形,点D在AC的上方与下方两种情况;
(2)∵∠A=30°、BC=6,
∴AB=2BC=12,
根据勾股定理,AC=6
①点D在AC的下方时,作DE⊥BC交BC的延长线于点E,
则DE=
Ac=3
,CE=9
∴BE=BC+CE=6+9=15
在Rt△BDE中,BD2=DE2+BE2,
∵BD>0
∴BD=6
;
②点D在AC的上方时,∵∠A=30°,
∴∠BAD=60°-30°=30°,
∴∠BAC=∠BAD,
∴AB⊥CD,
∴△ABD与△ABC关于AB成轴对称,
∴BD=BC,
∵BC=6,
∴BD=6;
综上所述,BD的长度为故答案为:6
或6.
(2)∵∠A=30°、BC=6,
∴AB=2BC=12,
根据勾股定理,AC=6
| 3 |
①点D在AC的下方时,作DE⊥BC交BC的延长线于点E,
则DE=
| 1 |
| 2 |
| 3 |
∴BE=BC+CE=6+9=15
在Rt△BDE中,BD2=DE2+BE2,
∵BD>0

∴BD=6
| 7 |
②点D在AC的上方时,∵∠A=30°,
∴∠BAD=60°-30°=30°,
∴∠BAC=∠BAD,
∴AB⊥CD,
∴△ABD与△ABC关于AB成轴对称,
∴BD=BC,
∵BC=6,
∴BD=6;
综上所述,BD的长度为故答案为:6
| 7 |
点评:本题考查了复杂作图,主要利用了过一点作已知直线的垂线,已知一边作等边三角形,都是基本作图,(2)题要注意分点D在AC的上方与下方两种情况讨论求解.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
下面说法正确的有( )
(1)正整数和负整数统称有理数;(2)0既不是正数,又不是负数;(3)0表示没有;(4)正数和负数统称有理数.
(1)正整数和负整数统称有理数;(2)0既不是正数,又不是负数;(3)0表示没有;(4)正数和负数统称有理数.
| A、4个 | B、3个 | C、2个 | D、1个 |
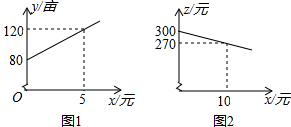 某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.
某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系.随着补贴数额x的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足如图2所示的一次函数关系.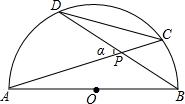 如图,C、D是以AB为直径的半圆上的两个点(不与A、B重合),连接DC、AC、DB,AC与BD交于点P,若∠APD=α,则
如图,C、D是以AB为直径的半圆上的两个点(不与A、B重合),连接DC、AC、DB,AC与BD交于点P,若∠APD=α,则 如图,点A为x轴负半轴上一点,用尺规作图(保留作图痕迹,不需要写作法)作出△ABC,满足:
如图,点A为x轴负半轴上一点,用尺规作图(保留作图痕迹,不需要写作法)作出△ABC,满足: 如图,是用七巧板拼成一个图形,其中③、⑥、①板的面积分别为S③,S⑥,S①,则 S③:S⑥:S①=
如图,是用七巧板拼成一个图形,其中③、⑥、①板的面积分别为S③,S⑥,S①,则 S③:S⑥:S①=