题目内容
 如图,点A为x轴负半轴上一点,用尺规作图(保留作图痕迹,不需要写作法)作出△ABC,满足:
如图,点A为x轴负半轴上一点,用尺规作图(保留作图痕迹,不需要写作法)作出△ABC,满足:(1)点B在y轴的正半轴上,点C在x轴的正半轴上,且∠BAC=45°、∠ABC=105°;
(2)在(1)的条件下,作出△ABC的垂心H;
(3)在(2)的条件下,若A点坐标为(-2,0),直接写出点H的坐标:
考点:作图—复杂作图
专题:
分析:(1)根据作一个角等于已知角的作图方法作图即可;
(2)三角形的垂心即为三角形三条高线的交点,由此作图即可;
(3)利用垂心的性质可求出∠AHB=30°,进而可求出OH的长,所以点H的坐标即可求出.
(2)三角形的垂心即为三角形三条高线的交点,由此作图即可;
(3)利用垂心的性质可求出∠AHB=30°,进而可求出OH的长,所以点H的坐标即可求出.
解答:解:(1)(2)如图所示:

(3)∵∠BAC=45°,∠ABC=105°,
∴∠OBC=60°,
∵AD⊥CD,
∴∠ACD=45°,
∴∠BCD=15°,
∵CE⊥AH,
∴∠EHC=75°,
∴∠HAO=15°,
∴∠AHO=30°,
∴AO=2,
∴AH=4,
∴OH=
=2
,
即点H坐标为(0,2
),
故答案为:(0,2
).

(3)∵∠BAC=45°,∠ABC=105°,
∴∠OBC=60°,
∵AD⊥CD,
∴∠ACD=45°,
∴∠BCD=15°,
∵CE⊥AH,
∴∠EHC=75°,
∴∠HAO=15°,
∴∠AHO=30°,
∴AO=2,
∴AH=4,
∴OH=
| 42-22 |
| 3 |
即点H坐标为(0,2
| 3 |
故答案为:(0,2
| 3 |
点评:本题考查了复杂作图,复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.

练习册系列答案
相关题目
如果60m表示“向东走60m”,那么“向西走40m”可以表示为( )
| A、-20m | B、-40m |
| C、20m | D、40m |
二次函数y=x2-2x-3上有两点:(-1,y1),(4,y2),下列结论正确的是( )
| A、y1>y2 |
| B、y1<y2 |
| C、y1=y2 |
| D、无法确定 |
在下列方程中,一定是关于x的一元二次方程的是( )
| A、x(x+3)=-1+x2 | ||
| B、ax2+5x+3=0 | ||
C、3x2+
| ||
| D、x2-2=6x |
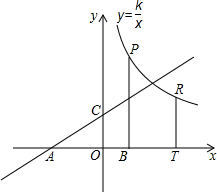 如图,直线y=
如图,直线y=
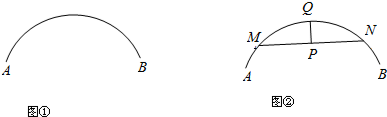
 a、b在数轴上的位置如图所示,那么化简|b-a|的结果是
a、b在数轴上的位置如图所示,那么化简|b-a|的结果是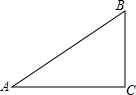 如图,已知Rt△ABC,∠C为直角,请你用尺规,按下列要求作图和计算(不必写画法,但保留作图痕迹)
如图,已知Rt△ABC,∠C为直角,请你用尺规,按下列要求作图和计算(不必写画法,但保留作图痕迹)