题目内容
6.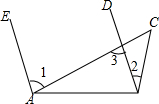 已知,如图,AE∥BD,∠1=3∠2,∠2=26°,求$\frac{1}{2}$∠C.
已知,如图,AE∥BD,∠1=3∠2,∠2=26°,求$\frac{1}{2}$∠C.
分析 根据两直线平行同旁内角互补的性质,使用三角形内角和定理可解.
解答  解:∵AE∥BD,
解:∵AE∥BD,
∴∠EAB+∠ABD=180°.
根据三角形内角和定理得:∠C=180°-∠CAB-∠ABC,
∵∠CAB=∠EAB-∠1,∠CBA=∠ABD+∠2,
∴∠C=180°-(∠EAB-∠1)-(∠ABD+∠2)=180°-(∠EAB+∠ABD)+(∠1-∠2).
∵∠1=3∠2,∠2=26°,
∴$\frac{1}{2}$∠C=$\frac{1}{2}$(180°-180°+2∠2)=∠2=26°.
点评 本题主要考查了三角形内角和定理,平行线的性质,熟练掌握平行线的性质即可得到结论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.若x:y=1:3,2y=3z,则$\frac{2x+y}{2x-y}$的值是( )
| A. | -5 | B. | -$\frac{10}{3}$ | C. | $\frac{10}{3}$ | D. | 5 |
14.方程x2=2x的解是( )
| A. | 2 | B. | 0 | C. | 0或2 | D. | 都不是 |
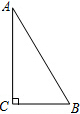 如图,在Rt△ABC中,∠C=90°,∠A=30°.
如图,在Rt△ABC中,∠C=90°,∠A=30°.