题目内容
3.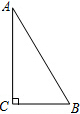 如图,在Rt△ABC中,∠C=90°,∠A=30°.
如图,在Rt△ABC中,∠C=90°,∠A=30°.(1)尺规作图:作边AB的垂直平分线交AB于点D,交AC于点E(不写画法,保留作图痕迹);
(2)若CE=3,求AE的长.
分析 (1)依据线段垂直平分线的作法画出图形即可;
(2)由线段垂直平分线的性质可知AE=EB,从而得到∠A=∠EBA=30°,然后可证明∠CBE=30°,故此AE=BE=2CE.
解答 解:(1)如图1所示:
(2)如图2所示:连接EB.
∵ED是AB的垂直平分线,
∴AE=EB.
∴∠A=∠EBA=30°.
∵∠A=30°,∠C=90°,
∴∠CBA=60°.
∴∠CBE=30°.
∴AE=BE=2CE=2×3=6.
∴AE=6.
点评 本题主要考查的是基本作图、线段垂直平分线的性质、含30°直角三角形的性质,证得∠EBC=30°是解题的关键.

练习册系列答案
相关题目
13.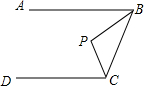 如图,AB∥CD,点P到AB、BC、CD距离都相等,则∠P=( )
如图,AB∥CD,点P到AB、BC、CD距离都相等,则∠P=( )
 如图,AB∥CD,点P到AB、BC、CD距离都相等,则∠P=( )
如图,AB∥CD,点P到AB、BC、CD距离都相等,则∠P=( )| A. | 120° | B. | 90° | C. | 75° | D. | 60° |
 如图,D为线段CB的中点,AD=8厘米,AB=10厘米,则CB的长度为4厘米.
如图,D为线段CB的中点,AD=8厘米,AB=10厘米,则CB的长度为4厘米.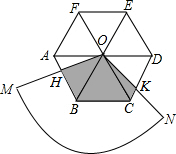 如图,圆心角为120°的扇形OMN,绕着正六边形ABCDEF的中心O旋转,OM交AB于H,ON交CD于K,OM>OA.
如图,圆心角为120°的扇形OMN,绕着正六边形ABCDEF的中心O旋转,OM交AB于H,ON交CD于K,OM>OA.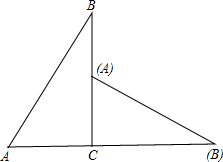 如图,在△ABC中,∠ACB=90°,AB=2BC=2,将△ABC绕点C顺时针旋转得到点B落在边AC上,则边AB在旋转过程中,所扫过的区域面积是$\frac{11}{12}π$+$\frac{\sqrt{3}}{4}$.
如图,在△ABC中,∠ACB=90°,AB=2BC=2,将△ABC绕点C顺时针旋转得到点B落在边AC上,则边AB在旋转过程中,所扫过的区域面积是$\frac{11}{12}π$+$\frac{\sqrt{3}}{4}$.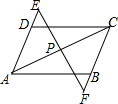 如图,AB=CD,AD=BC,P为AC上任一点,过P的直线分别交AD,CB的延长线于点E,F.
如图,AB=CD,AD=BC,P为AC上任一点,过P的直线分别交AD,CB的延长线于点E,F.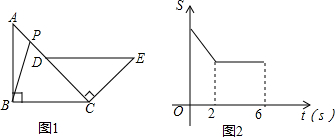
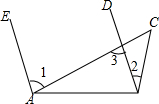 已知,如图,AE∥BD,∠1=3∠2,∠2=26°,求$\frac{1}{2}$∠C.
已知,如图,AE∥BD,∠1=3∠2,∠2=26°,求$\frac{1}{2}$∠C.