题目内容

15．已知$\frac{a}{2}$=$\frac{b}{3}$=$\frac{c}{4}$（a≠0），那么（a+b+c）：b等于（　　）
A．3B．2C．4D．5

分析 根据等式的性质，可用k表示a，用k表示b，用k表示c，再根据比的性质，可得答案．

解答 解：设$\frac{a}{2}$=$\frac{b}{3}$=$\frac{c}{4}$=k，得
a=2k，b=3k，c=4k．
（a+b+c）：b=（2k+3k+4k）：（3k）=（9k）：（3k）=3，
故选：A．

点评 本题考查了比例的性质，利用等式的性质得出a=2k，b=3k，c=4k是解题关键，又利用了比的性质．

练习册系列答案
相关题目
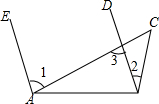5．如图1，在等腰Rt△ABC中，D为斜边AC边上一点，以CD为直角边，点C为直角顶点，向外构造等腰Rt△CDE．动点P从点A出发，以1个单位/s的速度，沿着折线A-D-E运动．在运动过程中，△BCP的面积S与运动时间t（s）的函数图象如图2所示，则BC的长是2$+\sqrt{2}$．
6．已知，如图，AE∥BD，∠1=3∠2，∠2=26°，求$\frac{1}{2}$∠C．
3．计算题：
（1）16÷（-2）3-（-$\frac{1}{8}$）×（-4）
（2）-24-12×（$\frac{2}{3}$-$\frac{3}{4}$-$\frac{3}{2}$×8）
10．画出数轴，并在数轴上画出表示下列各数的点：-$\frac{1}{2}$，0，-2.5，-|-5|，-3$\frac{1}{3}$．并用“＜”连接各数．
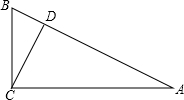20．如图所示，在Rt△ABC中，∠ACB=90°，CD⊥AB于D．
（1）请你写出图中有哪几对相似三角形；
（2）若BD=2，AD=8，请你选出最佳一对予以证明，并由此结论能直接求出CD的长．
7．把下列各数填入合适的括号中：
-23，0.5，-3，28，0，4，5，-5.2．
整数：{                         }
正数：{      　                 }
负分数：{                         }
正整数：{                         }
有理数：{                         }．
4．已知$\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=\frac{3}{5}$，b-2d+3f=50，那么a-2c+3e=30．
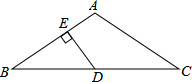5．在△ABC中，AB=AC，∠A=120°，D是BC的中点，DE⊥AB，垂足是E，则AE：BE=1：3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网