题目内容
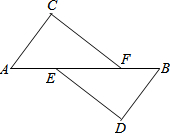 已知,如图:A、E、F、B在一条直线上,AE=BF,∠C=∠D,AC∥BD,
已知,如图:A、E、F、B在一条直线上,AE=BF,∠C=∠D,AC∥BD,求证:CF=DE.
考点:全等三角形的判定与性质
专题:证明题
分析:求出AF=BE,根据平行线性质求出∠A=∠B,根据AAS推出△ACF≌△BDE即可.
解答:证明:∵AE=BF,
∴AE+EF=BF+EF,
∴AF=BE,
∵AC∥BD,
∴∠A=∠B,
在△ACF和△BDE中
∴△ACF≌△BDE,
∴CF=DE.
∴AE+EF=BF+EF,
∴AF=BE,
∵AC∥BD,
∴∠A=∠B,
在△ACF和△BDE中
|
∴△ACF≌△BDE,
∴CF=DE.
点评:本题考查了全等三角形的性质和判定,平行线的性质的应用,解此题的关键是推出△ACF≌△BDE,注意:全等三角形的对应边相等,对应角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,点E是?ABCD边AD上一点,且AE=
如图,点E是?ABCD边AD上一点,且AE= 如图,函数y=-kx(k≠0)与y=-
如图,函数y=-kx(k≠0)与y=-