题目内容
2．若a2+a+1=0，求a+a2+a3+a4+a5+a6+…a2016的值．分析 首先将a+a2+a3+…+a2016变形为：a（a2+a+1）+a4（a2+a+1）…+a2014（a2+a+1），然后将a2+a+1=0代入即可求得答案．
解答 解：∵a2+a+1=0，
∴a+a2+a3+a4+a5+a6+…a2016
=a（a2+a+1）+a4（a2+a+1）…+a2014（a2+a+1）
=0．
点评 此题考查了因式分解的应用，分组分解与整体代入是求得答案的关键．
练习册系列答案
相关题目
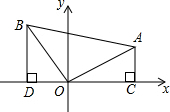△ABO为等腰直角三角形，斜边AB=4，过A作AC⊥x轴于C，AC=$\frac{1}{2}$AO，则点A的坐标是（2，$\sqrt{2}$），点B的坐标是（-$\sqrt{2}$，2）．
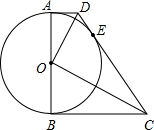已知：如图，AD、BC与⊙O切于A、B，且AD∥BC，若∠COD=90°