Question

10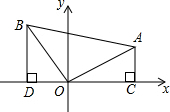．△ABO为等腰直角三角形，斜边AB=4，过A作AC⊥x轴于C，AC=$\frac{1}{2}$AO，则点A的坐标是（2，$\sqrt{2}$），点B的坐标是（-$\sqrt{2}$，2）．

Answer 1

分析 根据等腰直角三角形的性质得出OA=$2\sqrt{2}$，利用含30°的直角三角形的性质解答即可．

解答 解：∵△ABO为等腰直角三角形，斜边AB=4，
∴OA=$2\sqrt{2}$，
∵AC⊥x轴于C，AC=$\frac{1}{2}$AO，
∴AC=$\sqrt{2}$，OC=2，
∴点A的坐标为（2，$\sqrt{2}$），
在△BDO与△OAC中，
$\left\{\begin{array}{l}{∠BDO=∠OCA}\\{∠DOB=∠CAO}\\{OB=OA}\end{array}\right.$，
∴△BDO≌△OAC（AAS），
∴OD=AC，BD=OC，
所以点B的坐标为（-$\sqrt{2}$，2），
故答案为：（2，$\sqrt{2}$），（-$\sqrt{2}$，2）

点评 此题主要考查了全等三角形的判定与性质，全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．