题目内容
一个口袋中装有5个红球，3个白球，1个绿球，摸到白球的频率______摸到绿球的频率(填“大于”“小于”或“等于”)
大于
【解析】由题意知这个口袋中装有5个红球，3个白球，1个绿球，共有5+3+1=9个球，摸到红球的概率是，摸到白球的概率是，摸到红球的概率是，因此，摸到白球的概率大于摸到绿球的概率.
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
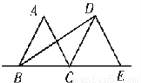
如图，△ABC和△DCE都是边长为2的等边三角形，点B，C，E在同一条直线上，连接BD，则BD的长为（ ）
A. 18 B. 3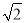
C. 12 D. 2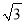
D
【解析】过点D作DF⊥EC于点F，利用正三角形的性质得出CF=1，BF=3，再利用勾股定理求出DF==，则可得BD=．
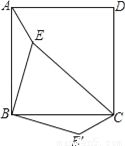
故选：D. 如图，点E是正方形ABCD内的一点，连接AE、BE、CE，将△ABE绕点B顺时针旋转90°到△CBE′的位置．若AE=1，BE=2，CE=3，则∠BE′C=__度．
135
【解析】试题分析：首先根据旋转的性质得出，△EBE′是直角三角形，进而得出∠BEE′=∠BE′E=45°，即可得出答案．
【解析】
连接EE′
∵△ABE绕点B顺时针旋转90°到△CBE′
∴∠EBE′是直角，∴△EBE′是直角三角形，
∵△ABE与△CE′B全等
∴BE=BE′=2，∠AEB=∠BE′C
∴∠BEE′=∠BE′E=45°，
... 如图，在平行四边形ABCD中，分别以AB、AD为边向外作等边△ABE、△ADF，延长CB交AE于点G，点G在点A、E之间，连接CE、CF，EF，则以下四个结论一定正确的是：①△CDF≌△EBC；②∠CDF=∠EAF；③△ECF是等边△；④CG⊥AE（ ）
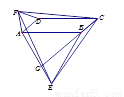
A. 只有①② B. 只有①②③ C. 只有③④ D. ①②③④
B
【解析】根据题意，结合图形，对选项一一求证，判定正确选项
【解析】
在□ABCD中，∠ADC=∠ABC，AD=BC，CD=AB，
∵△ABE、△ADF都是等边三角形，
∴AD=DF，AB=EB，∠ADF=∠ABE=60°，
∴DF=BC，CD=BC，
∴∠CDF=360°-∠ADC-60°=300°-∠ADC，
∠EBC=360°-∠ABC-60°=300°-∠ABC，... 如图是若干张卡片，它们的背面都一样，现将它们背面朝上，从中任意摸一张卡片，摸到几号卡片的频率大？
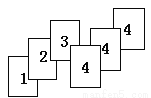
摸到4号卡片的频率大.
【解析】试题分析: 本题考察可能性大小的应用，根据不同编号卡片的数量求出不同编号卡片被抽到的概率是解答本题的关键.
解答：因为给出的六张卡片中，1号卡片有1张，2号有1张，3号有1张，4号有3张.所以摸到1号卡片的频率为，摸到2号卡片的频率为，摸到3号卡片的频率为，摸到4号卡片的频率为.所以，摸到4号卡片的频率大. 下列事件中，随机事件是（ ）
A. 没有水分，种子仍能发芽 B. 等腰三角形两个底角相等
C. 从13张红桃扑克牌中任抽一张，是红桃A D. 从13张方块扑克牌中任抽一张，是红桃10
C
【解析】对于A，没有水分，种子仍能发芽，这是一个不可能事件，发生的可能性为0；对于B，是一个必然事件，发生的可能性是1；对于C，是一个随机事件，发生的可能性是；对于D，是一个不可能事件，发生的可能性是0.发生的可能性是0和1的，都属于必然事件.
故选C. 爸爸买彩票，（ ）中奖.
A. 一定 B. 可能 C. 不可能 D. 以上都不对
B
【解析】对于买彩票，一定有人中奖，这是一个必然事件；但是对于是谁中奖，这是一个随机事件.所以“爸爸买彩票，中奖”这是一个随机事件.
故选B. 小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是（ ）
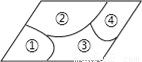
A. ①，② B. ①，④ C. ③，④ D. ②，③
D
【解析】分析：本题考查的是平行四边形的性质.
解析：破碎的玻璃中的②和③是连接的，可以得到四边形的大小.
故选B. 已知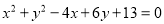
，求
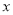和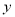
的值分别是多少？
x=2;y=-3
【解析】试题分析：运用完全平方公式把x²+y²-4x+6y+13化成(x-2)²+(y+3)²的形式即可知答案.
试题解析：由x²+y²-4x+6y+13=0 ，
得(x-2)²+(y+3)²=0，
∴x-2=0，y+3=0，
∴x=2，y=-3.