题目内容
17.一个不透明的口袋里装有分别标有汉字“大”、“雅”、“丹”、“棱”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀再摸球.(1)若从中任取一个球,球上的汉字刚好是“丹”的概率为多少?
(2)甲从中任取一球,不放回,再从中任取一球,请用树状图的方法,求出甲取出的两个球上的汉字恰能组成“大雅”或“丹棱”的概率P1;
(3)乙从中任取一球,记下汉字后再放回袋中,然后再从中任取一球,记下汉字,则乙取出的两个球上的汉字恰能组成“大雅”或“丹棱”的概率为P2,请指出P1,P2的大小关系.
分析 (1)直接根据概率公式求解;
(2)先画树状图展示所有12种等可能的结果数,再找出能组成“大雅”或“丹棱”的结果数,然后根据概率公式求解;
(3)先画树状图展示所有16种等可能的结果数,再找出能组成“大雅”或“丹棱”的结果数,然后根据概率公式求解,再比较P1与P2的大小.
解答 解:(1)从中任取一个球,球上的汉字刚好是“丹”的概率=$\frac{1}{4}$;
(2)画树状图为: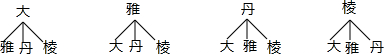
共有12种等可能的结果数,其中能组成“大雅”或“丹棱”的结果数为4,
所以能组成“大雅”或“丹棱”的概率P1=$\frac{4}{12}$=$\frac{1}{3}$;
(3)画树状图为:
共有16种等可能的结果数,其中能组成“大雅”或“丹棱”的结果数为4,
所以恰能组成“大雅”或“丹棱”的概率为P2=$\frac{4}{16}$=$\frac{1}{4}$,
所以P1>P2.
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.一个物体向西移动5米记作-5米,这个物体又移动了若干米,停留在两次移动前的位置的西边1米处.能反映这个物体第二次移动的方向和路程的算式是( )
| A. | -1-(-5) | B. | 1+(-5) | C. | -1+(-5) | D. | 1-(-5) |
5.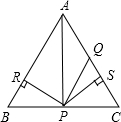 如图所示,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS中( )
如图所示,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS中( )
 如图所示,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS中( )
如图所示,在△ABC中,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS中( )| A. | 全部正确 | B. | 仅①和③正确 | C. | 仅①正确 | D. | 仅①和②正确 |
6.下列各组线段中,能构成直角三角形的是( )
| A. | 4cm,5cm,6cm | B. | 1cm,1cm,$\sqrt{2}$cm | C. | 6cm,8cm,11cm | D. | 5cm,12cm,23cm |
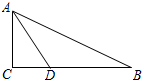 已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
已知,如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.