题目内容
18.已知二次函数y=-x2+2mx-2m2-3(m为常数).(1)求证:不论m为何值,该二次函数图象与x轴没有公共点;
(2)如果把该函数图象沿y轴向上平移4个单位后,得到的函数图象与x轴只有一个公共点,试求m的值.
分析 (1)求出根的判别式,即可得出答案;
(2)先化成顶点式,根据顶点坐标和平移的性质得出即可.
解答 解:(1)令y=0,-x2+2mx-2m2-3=0,
则a=-1,b=2m,c=-2m2-3.
∴b2-4ac=(2m)2-4(-1)(-2m2-3)=-4m2-12,
∵-4m2≤0,
∴-4m2-12<0,即b2-4ac<0,
∴一元二次方程-x2+2mx-2m2-3=0没有实数根,
∴不论m为何值,该二次函数图象与x轴没有公共点;
(2)将二次函数y=-x2+2mx-2m2-3配方得:
y=-(x-m)2-m2-3
∴该二次函数图象的顶点坐标为( m,-m2-3),
∵将函数图象沿y轴向上平移4个单位后,得到的函数图象与x轴只有一个公共点,
∴-m2-3+4=0,
解得m=±1.
点评 本题考查了二次函数和x轴的交点问题,根的判别式,平移的性质,二次函数的图象与几何变换的应用,主要考查学生的理解能力和计算能力,题目比较好,有一定的难度.

练习册系列答案
相关题目
13. 如图是某个几何体的三视图,该几何体是( )
如图是某个几何体的三视图,该几何体是( )
 如图是某个几何体的三视图,该几何体是( )
如图是某个几何体的三视图,该几何体是( )| A. | 三棱柱 | B. | 三棱锥 | C. | 圆锥 | D. | 圆柱 |
7.5月14日-15日“一路一带”国际合作高峰论坛在北京举行,世界的目光再次聚焦中国,某网站调查显示截至5月22日有174万余人关注此次峰会,174万用科学记数法可表示为( )
| A. | 0.174×107 | B. | 1.74×106 | C. | 1.74×105 | D. | 17.4×105 |
 尺规作图:如图,线段AB,BC,∠ABC=90°.求作:矩形ABCD.小明的作图过程如下:
尺规作图:如图,线段AB,BC,∠ABC=90°.求作:矩形ABCD.小明的作图过程如下:
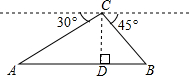 如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度为200米,点A、B、C在同一直线上,则AB两点间的距离是200($\sqrt{3}$+1)米(结果保留根号).
如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度为200米,点A、B、C在同一直线上,则AB两点间的距离是200($\sqrt{3}$+1)米(结果保留根号).