题目内容
2.化简与计算:(1)$\sqrt{75{x}^{3}{y}^{2}}$( x≥0,y≥0);
(2)$\sqrt{103}$×$\frac{\sqrt{3}}{6}$+$\sqrt{32}$÷$\sqrt{\frac{1}{2}}$.
分析 (1)利用二次根式的性质化简;
(2)利用二次根式的乘除法法则运算.
解答 解:(1)原式=5xy$\sqrt{3x}$;
(2)原式=$\frac{\sqrt{108×3}}{6}$+$\sqrt{32×2}$
=3+8
=11.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
12.1+0.2%等于( )
| A. | 1.2% | B. | 1.02% | C. | 1.002% | D. | 100.2% |
13.在弹簧限度内,弹簧挂上物体后弹簧的长度与所挂物体的质量之间的关系如下表:
(1)上表中,自变量是物体的质量,因变量是弹簧的长度.
(2)弹簧不挂物体时的长度是12cm.
(3)如果用x表示弹性限度内物体的质量,用y表示弹簧的长度,那么随着x的变化,y的变化趋势是增长.
(4)写出y与x的关系式y=0.5x+12.
(5)如果弹簧最大挂重量为25千克,你能预测当挂重为14千克时,弹簧的长度是多少?
| 所挂物体的质量/千克 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 弹簧的长度/cm | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 | 15 | 15.5 | 16 |
(2)弹簧不挂物体时的长度是12cm.
(3)如果用x表示弹性限度内物体的质量,用y表示弹簧的长度,那么随着x的变化,y的变化趋势是增长.
(4)写出y与x的关系式y=0.5x+12.
(5)如果弹簧最大挂重量为25千克,你能预测当挂重为14千克时,弹簧的长度是多少?
10.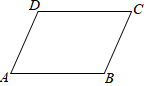 如图,AD=BC,要使四边形ABCD是平行四边形,还需补充的一个条件,下列错误的是( )
如图,AD=BC,要使四边形ABCD是平行四边形,还需补充的一个条件,下列错误的是( )
 如图,AD=BC,要使四边形ABCD是平行四边形,还需补充的一个条件,下列错误的是( )
如图,AD=BC,要使四边形ABCD是平行四边形,还需补充的一个条件,下列错误的是( )| A. | AB=DC | B. | AD∥BC | C. | ∠A+∠B=180° | D. | ∠A+∠D=180° |
17.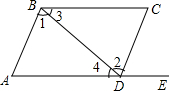 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④AD∥BC,且∠A=∠C.其中,能推出AB∥DC的条件为( )
如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④AD∥BC,且∠A=∠C.其中,能推出AB∥DC的条件为( )
 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④AD∥BC,且∠A=∠C.其中,能推出AB∥DC的条件为( )
如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④AD∥BC,且∠A=∠C.其中,能推出AB∥DC的条件为( )| A. | ①④ | B. | ②③ | C. | ①③ | D. | ①③④ |
11.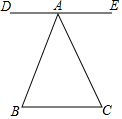 如图,ED∥BC,∠B=∠C,则下列正确的是( )
如图,ED∥BC,∠B=∠C,则下列正确的是( )
 如图,ED∥BC,∠B=∠C,则下列正确的是( )
如图,ED∥BC,∠B=∠C,则下列正确的是( )| A. | ∠BAE=∠DAC | B. | ∠BAE=∠ACB | C. | ∠ABC=∠DAC | D. | ∠BAC=∠DAC |
12.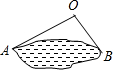 如图,为估计池塘岸边A,B的距离,小明在池塘的一侧选取一点O,测得OA=15米,OB=10米,A,B间的距离可能是( )
如图,为估计池塘岸边A,B的距离,小明在池塘的一侧选取一点O,测得OA=15米,OB=10米,A,B间的距离可能是( )
 如图,为估计池塘岸边A,B的距离,小明在池塘的一侧选取一点O,测得OA=15米,OB=10米,A,B间的距离可能是( )
如图,为估计池塘岸边A,B的距离,小明在池塘的一侧选取一点O,测得OA=15米,OB=10米,A,B间的距离可能是( )| A. | 30米 | B. | 25米 | C. | 20米 | D. | 5米 |
