题目内容
8. 如图,将边长为3的正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
如图,将边长为3的正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.(1)求证:△AOG≌△ADG;
(2)求∠PAG的度数;
(3)当∠1=∠2时,求OG的长.
分析 (1)由正方形得出边相等,角为90°,再根据HL即可证明△AOG≌△ADG;
(2)由△AOG≌△ADG和△ADP≌△ABP,得出对应角相等,即可得出结果;
(3)根据三角形全等得出角相等,证出∠AGO=∠AGD=∠PGC=60°,得出∠1=∠2=30°,根据三角函数求出OG的长.
解答 (1)证明:∵正方形ABCO≌正方形ADEF,
∴∠AOG=∠ADG=90°,OA=AD,
在Rt△AOG和Rt△ADG中,
$\left\{\begin{array}{l}{AG=AG}\\{OA=AD}\end{array}\right.$,
∴Rt△AOG≌Rt△ADG(HL);
(2)解:由(1)同理可证△ADP≌△ABP,则∠DAP=∠BAP,
∵△AOG≌△ADG,
∴∠1=∠DAG,
又∵∠1+∠DAG+∠DAP+∠BAP=90°,
∴2∠DAG+2∠DAP=90°,
即∠DAG+∠DAP=45°.
∴∠PAG=∠DAG+∠DAP=45°;
(3)解:∵△AOG≌△ADG,
∴∠AGO=∠AGD.
又∵∠1+∠AGO=90°,∠2+∠PGC=90°,∠1=∠2,
∴∠AGO=∠AGD=∠PGC,
又∵∠AGO+∠AGD+∠PGC=180°,
∴∠AGO=∠AGD=∠PGC=60°.
∴∠1=∠2=30°,
在Rt△AOG中,AO=3,OG=AOtan30°=$\sqrt{3}$.
点评 本题考查了正方形的性质、全等三角形的判定与性质以及旋转的性质;证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
18.化简(a+$\frac{1}{2}$)-2(3a-$\frac{2}{3}$)的结果是( )
| A. | -5a+$\frac{11}{6}$ | B. | -5a+$\frac{7}{6}$ | C. | -7a+$\frac{1}{3}$ | D. | -5a-$\frac{5}{6}$ |
16.今年春节“黄金周”全市接待游客总数为833100人次,833100用科学记数法表示为( )
| A. | 0.833×106 | B. | 83.31×105 | C. | 8.331×105 | D. | 8.331×104 |
3. 如图,线段DE是△ABC的中位线,∠B=60°,则∠ADE的度数为( )
如图,线段DE是△ABC的中位线,∠B=60°,则∠ADE的度数为( )
 如图,线段DE是△ABC的中位线,∠B=60°,则∠ADE的度数为( )
如图,线段DE是△ABC的中位线,∠B=60°,则∠ADE的度数为( )| A. | 80° | B. | 70° | C. | 60° | D. | 50° |
 如图,梯形ABCD中,AD∥BC,AB=CD=6,AD=5,BC=11,则梯形ABCD的面积为24$\sqrt{3}$.
如图,梯形ABCD中,AD∥BC,AB=CD=6,AD=5,BC=11,则梯形ABCD的面积为24$\sqrt{3}$.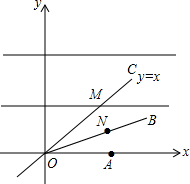 如图点A(2,0)点N在射线OB上运动,点M是直线y=x上一动点,OB为∠AOC的角平分线,求AN+MN的最小值,要画出图象.
如图点A(2,0)点N在射线OB上运动,点M是直线y=x上一动点,OB为∠AOC的角平分线,求AN+MN的最小值,要画出图象.