题目内容
18.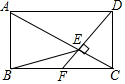 如图,在矩形ABCD中,F是BC边的中点,DF⊥AC,垂足为点E,连接BE,分析下列四个结论:①△CEF∽△CBA;②BE=AB;③AE=2CE;④tan∠ACB=$\sqrt{2}$,其中正确的个数有( )
如图,在矩形ABCD中,F是BC边的中点,DF⊥AC,垂足为点E,连接BE,分析下列四个结论:①△CEF∽△CBA;②BE=AB;③AE=2CE;④tan∠ACB=$\sqrt{2}$,其中正确的个数有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 根据矩形的性质得到AD∥BC,∠ADC=90°,AD=BC,DE⊥AC于点E,于是得到△CEF∽△CBA,故①正确;连接AF,推出A、B、F、E四点共圆,得到∠AEB=∠AFB,根据全等三角形的性质得到∠AFB=∠CFD,得到∠BAE=∠BEA,根据等腰三角形的判定得到BA=BE,故②正确.根据相似三角形的性质得到AE=2CE,故③正确,设CE=a,AE=2a,由DE2=AE•CE=2a2,得D=$\sqrt{2}$a,根据三角函数的定义即可得到tan∠ACB=tan∠EAD=$\frac{DE}{AE}$=$\frac{\sqrt{2}a}{2a}$=$\frac{\sqrt{2}}{2}$,故④错误.
解答 解:∵四边形ABCD是矩形,
∴AD∥BC,∠ADC=90°,AD=BC,DE⊥AC于点E,
∵∠ACB=∠ECF,∠ADC=∠CEF=90°,
∴△CEF∽△CBA,故①正确;
连接AF,∵∠ABF+∠AEF=90°,
∴A、B、F、E四点共圆,
∴∠AEB=∠AFB,
∵F是BC边的中点,
∴BF=CF,
在△ABF与△DCF中,$\left\{\begin{array}{l}{AB=CD}\\{∠ABF=∠DCF}\\{BF=CF}\end{array}\right.$,
∴△ABF≌△CDF,
∴∠AFB=∠CFD,
∵∠BAE+∠BFE=180°,∠BFE+∠CFD=180°,
∴∠BAE=∠CFD,
∴∠BAE=∠BEA,
∴BA=BE,故②正确.
∵AD∥BC,
∴△CEF∽△ADE,
∴$\frac{CF}{AD}$=$\frac{CE}{AE}$,
∵CF=$\frac{1}{2}$BC=$\frac{1}{2}$AD,
∴$\frac{AE}{EC}$=$\frac{AD}{CF}$=2,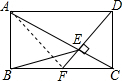
∴AE=2CE,故③正确,
设CE=a,AE=2a,由DE2=AE•CE=2a2,得DE=$\sqrt{2}$a,
∴tan∠ACB=tan∠EAD=$\frac{DE}{AE}$=$\frac{\sqrt{2}a}{2a}$=$\frac{\sqrt{2}}{2}$,故④错误.
故选B.
点评 本题考查了相似三角形的判定和性质,矩形的性质,全等三角形的判定和性质、四点共圆等知识,正确的作出辅助线是解题的关键,学会利用此时解决问题,属于中考常考题型.

| A. | y>0且y随x的增大而减小 | B. | y>0且y随x的增大而增大 | ||
| C. | y<0且y随x的增大而减小 | D. | y<0且y随x的增大而增大 |
| A. | 2x•(-xy)2=-2x3y | B. | (-x2)3÷(-x3)2=1 | ||
| C. | ($\frac{3}{4}$a3-$\frac{1}{2}$b)•2ab=$\frac{3}{2}$a4b-ab2 | D. | (3m-1)2=9m2-1 |
 如图,OE平分∠AOC,OF平分∠BOC,且∠BOC=60°,若∠AOC+∠EOF=156°,则∠EOF的度数是( )
如图,OE平分∠AOC,OF平分∠BOC,且∠BOC=60°,若∠AOC+∠EOF=156°,则∠EOF的度数是( )| A. | 88° | B. | 30° | C. | 32° | D. | 48° |
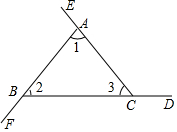 用两种方法证明“三角形的外角和等于360°”如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角.
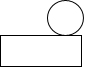
用两种方法证明“三角形的外角和等于360°”如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角. 我国古代数学家利用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,如图所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( )
我国古代数学家利用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体,如图所示的几何体是可以形成“牟合方盖”的一种模型,它的主视图是( )


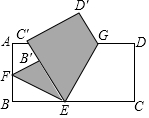 将一长方形纸片按如图所示的方式折叠,EF,EG为折痕,若∠BEF=30°,AB=3$\sqrt{3}$,则EG=( )
将一长方形纸片按如图所示的方式折叠,EF,EG为折痕,若∠BEF=30°,AB=3$\sqrt{3}$,则EG=( )