题目内容
16.已知m、n分别是$6-\sqrt{13}$的整数部分和小数部分,求m、n的值,并求代数式${n^2}-\frac{2n}{m}-{m^2}$的值.分析 首先判断出$\sqrt{13}$在3和4之间,即6-$\sqrt{13}$的整数部分m=2,则n=4-$\sqrt{13}$,然后把a和b的值代入代数式求值即可.
解答 解:∵$\sqrt{9}$<$\sqrt{13}$<$\sqrt{16}$,
∴$\sqrt{13}$的整数部分在3和4之间,
∴6-$\sqrt{13}$的整数部分m=2,n=4-$\sqrt{13}$,
${n^2}-\frac{2n}{m}-{m^2}$
=$(4-\sqrt{13})^{2}-\frac{2(4-\sqrt{13})}{2}-{2}^{2}$
=16-8$\sqrt{13}$+13-4+$\sqrt{13}$-4
=21-7$\sqrt{13}$.
点评 本题主要考查了代数式求值,涉及到比较有理数和无理数的大小,解题的关键在于用正确的形式表示出6-$\sqrt{13}$的整数部分和小数部分,然后代入求值即可.

练习册系列答案
相关题目
 由5个完全相同的正方体组成的立体图形如图所示,则它的俯视图是( )
由5个完全相同的正方体组成的立体图形如图所示,则它的俯视图是( )



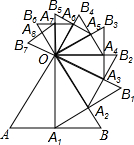 已知等边△OAB的边长为1,以AB边上的高OA1为边,按逆时针方向作等边△OA1B1,A1B1与OB相交于点A2,再以OA2为边按逆时针方向作等边△OA2B2,A2B2与OB1相交于点A3,按此操作进行下去,得到△OA3B3,△OA4B4,…,△OAnBn,如图,求得△OA7B7的周长是3($\frac{\sqrt{3}}{2}$)7.
已知等边△OAB的边长为1,以AB边上的高OA1为边,按逆时针方向作等边△OA1B1,A1B1与OB相交于点A2,再以OA2为边按逆时针方向作等边△OA2B2,A2B2与OB1相交于点A3,按此操作进行下去,得到△OA3B3,△OA4B4,…,△OAnBn,如图,求得△OA7B7的周长是3($\frac{\sqrt{3}}{2}$)7. 如图,在正六边形ABCDEF中,△ABC的面积为4,则△ABE的面积为8.
如图,在正六边形ABCDEF中,△ABC的面积为4,则△ABE的面积为8. 如图,在等腰直角△ABC中,∠ACB=90°,点D、F为BC边上的两点,CD=BF,连接AD,过点C作AD的垂线角AB于点E,连接EF.
如图,在等腰直角△ABC中,∠ACB=90°,点D、F为BC边上的两点,CD=BF,连接AD,过点C作AD的垂线角AB于点E,连接EF. 如图,若DE∥BC,AD:BD=5:3,DE=10cm,则BC=16cm.
如图,若DE∥BC,AD:BD=5:3,DE=10cm,则BC=16cm.