题目内容
如图，直线AB与直线CD相交于点O，OE垂直于AB，∠EOD=30°，则∠BOC=考点：垂线,对顶角、邻补角
专题：
分析：根据垂直的定义可得∠BOE=90°，然后列式计算即可求出∠BOD，再根据邻补角互补求出∠BOC即可．
解答：解：∵EO⊥AB，
∴∠BOE=90°，
∵∠EOD=30°，
∴∠BOD=90°-∠EOD=90°-30°=60°，
∴∠BOC=180°-∠BOD=180°-60°=120°，
故答案为：120°．
∴∠BOE=90°，
∵∠EOD=30°，
∴∠BOD=90°-∠EOD=90°-30°=60°，
∴∠BOC=180°-∠BOD=180°-60°=120°，
故答案为：120°．
点评：本题主要考查了垂线的定义，对顶角相等，邻补角互补的性质，是基础题，准确识图是解题的关键．
练习册系列答案
相关题目
如图，AB∥CD，点G、F分别在AB、CD上，FE平分∠GFD交AB于点E，∠EGF=40°，则∠BEF=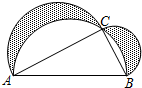
如图，在Rt△ABC中，两直角边AC=15，BC=8，在AB的同侧，分别以AB，BC，AC为直径作三个半圆，则阴影部分的面积=
如图，矩形ABCD中，
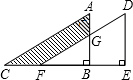如图，将直角三角形ABC沿CB方向平移BE的距离后，得到直角三角形DEF．已知AG=4，BE=6，DE=12，则阴影部分的面积为已知点P（x，y）的坐标满足二元一次方程组
，则点P所在的象限为（ ）
|
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |