题目内容
1.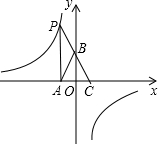 如图,点P是反比例函数y=$\frac{k}{x}$(k<0)图象上的点,PA垂直x轴于点A(-1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB=$\sqrt{5}$,则k的值等于( )
如图,点P是反比例函数y=$\frac{k}{x}$(k<0)图象上的点,PA垂直x轴于点A(-1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB=$\sqrt{5}$,则k的值等于( )| A. | 2 | B. | -2 | C. | -4 | D. | -6 |
分析 根据题意过点P作PE⊥y轴于点E,得出△PBE≌△CBO(AAS),进而求出P点坐标即可得出答案.
解答 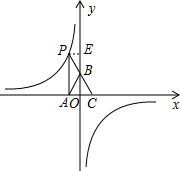 解:过点P作PE⊥y轴于点E,
解:过点P作PE⊥y轴于点E,
∵PA垂直x轴于点A(-1,0),点C的坐标为(1,0),
∴PE=CO=AO=1,
∵AB=$\sqrt{5}$,
∴BO=2,
在△PBE和△CBO中
∵$\left\{\begin{array}{l}{∠PBE=∠CBO}\\{∠BEP=∠BOC}\\{PE=CO}\end{array}\right.$,
∴△PBE≌△CBO(AAS),
∴BE=BO=2,
∴P点坐标为:(-1,4),
∴k=-1×4=-4.
故选C.
点评 此题主要考查了反比例函数图象上点的坐标特点,得出P点纵坐标是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.生物具有遗传多样性,遗传信息大多储存在DNA分子上,一个DNA分子直径约为0.000000201cm,这个数量用科学记数法可表示为( )
| A. | 0.201×10-6cm | B. | 2.01×10-6cm | C. | 0.201×10-7cm | D. | 2.01×10-7cm |
16.下列命题是假命题的是( )
| A. | 两直线平行,同位角相等 | |
| B. | 两点之间线段最短 | |
| C. | 对顶角相等 | |
| D. | 过一点有且只有一条直线与已知直线平行 |
6.已知ab>15,且a=-5,则b的取值范围是 ( )
| A. | b>3 | B. | b<3 | C. | b>-3 | D. | b<-3 |
13.下列团中既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
10. 直线AB、CD、EF相交于O,则∠1+∠2+∠3=( )
直线AB、CD、EF相交于O,则∠1+∠2+∠3=( )
 直线AB、CD、EF相交于O,则∠1+∠2+∠3=( )
直线AB、CD、EF相交于O,则∠1+∠2+∠3=( )| A. | 90° | B. | 120° | C. | 180° | D. | 140° |