题目内容
3.若抛物线y=(1+m)xm2-1的开口向下.(1)求m的值;
(2)若A(-1,y1),B(-2,y2)在抛物线上,试比较y1与y2的大小.
分析 (1)由开口向下得出1+m<0,二次函数的意义得出m2-1=2,两者联立求得答案即可;
(2)对称轴为0,所以点A(-1,y1),B(-2,y2)在对称轴的左侧,利用性质得出答案即可.
解答 解:(1)由题意得1+m<0,m2-1=2,
解得m=±$\sqrt{3}$,m<-1,
因此m=-$\sqrt{3}$.
(2)∵抛物线的对称轴是x=0,
∴当x<0时,y随着x的增大而增大,
∵-1>-2,
∴y1>y2.
点评 本题考查了二次函数的性质与二次函数的意义,掌握二次函数的性质是解决问题的关键.

练习册系列答案
相关题目
 如图,△EFG的三条边相等,三个内角也相等,且EH=FI=GJ,找出图中一对全等三角形,并说明理由.
如图,△EFG的三条边相等,三个内角也相等,且EH=FI=GJ,找出图中一对全等三角形,并说明理由. 如图,把两个全等的矩形ABCD和矩形CEFG拼成如图所示的图案,求∠ACF,∠AFC的度数.
如图,把两个全等的矩形ABCD和矩形CEFG拼成如图所示的图案,求∠ACF,∠AFC的度数.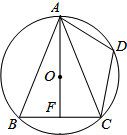 如图,⊙O是△ABC的外接圆,AO⊥BC于点F,D为$\widehat{AC}$的中点,且$\widehat{CD}$的度数为72°,求∠BAF的度数.
如图,⊙O是△ABC的外接圆,AO⊥BC于点F,D为$\widehat{AC}$的中点,且$\widehat{CD}$的度数为72°,求∠BAF的度数.