题目内容
3.某社区调查社区居民双休日的学习状况,采取下列调查方式:①从一幢高层住宅楼中选取200名居民;②从不同住层楼中随机选取200名居民;③选取社区内的200名在校学生.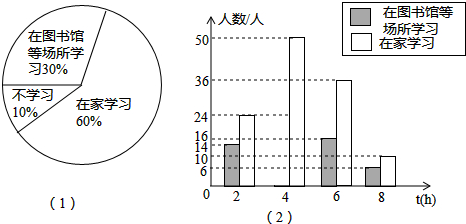
(1)上述调查方式最合理的是②(填序号);
(2)将最合理的调查方式得到的数据制成扇形统计图(如图(1))和频数分布直方图(如图(2)).
①请补全频数分布直方图(直接画在图(2)中);
②在这次调查中,200名居民中,“在家学习”的有24人;
③在图(1)中,“不学习”这一扇形的圆心角是120;
(3)请估计该社区1000名居民中双休日学习时间不少于4h的人数.
分析 (1)抽样调查时,为了获得较为准确的调查结果,所以抽样时要注意样本的代表性和广泛性;
(2)①先求出在图书馆等场所学习的总人数,再求出在图书馆等场所学习4小时的人数,然后补充统计图即可;
②利用200名居民中,在家学习的占60%即可求出答案;
(3)首先利用频数分布直方图中的有关数据,计算出双休日学习时间不少于4h的人数占样本的百分比,然后利用样本估计总体,即可算出该社区2000名居民中双休日学习时间不少于4h的人数.
解答 解:(1)调查方式最合理的是②;
故答案为:②;
(2)①200×30%-14-16-6=24,补充图形如下:
②在家学习的有200×60%=120(人),
故答案为:120;
(3)根据题意得:$\frac{24+50+16+36+6+10}{200}$×2000=1420(人),
答:该社区2000名居民双休日学习时间不少于4h的人数为1420人.
点评 此题考查了用样本估计总体和扇形统计图及相关计算,用到的知识点为:概率=所求情况数与总情况数之比.部分数目=总体数目乘以相应百分比.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
13.下列命题中真命题的个数有( )
①小朋友荡秋千可以看做是平移运动;
②两条直线被第三条直线所截,同位角相等;
③过一点有且只有一条直线与已知直线平行;
④不是对顶角的角不相等.
①小朋友荡秋千可以看做是平移运动;
②两条直线被第三条直线所截,同位角相等;
③过一点有且只有一条直线与已知直线平行;
④不是对顶角的角不相等.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14. 菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )
菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )
 菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )
菱形OACB在平面直角坐标系中位置如图所示,点C的坐标是(8,0),点A的纵坐标是1,则点B的坐标是( )| A. | (4,1) | B. | (4,-1) | C. | (1,4) | D. | (1,-4) |
11.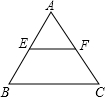 如图所示,刘伯伯家有一块等边三角形的空地,已知E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围起来放养小鸡,则需用篱笆的长是( )
如图所示,刘伯伯家有一块等边三角形的空地,已知E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围起来放养小鸡,则需用篱笆的长是( )
 如图所示,刘伯伯家有一块等边三角形的空地,已知E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围起来放养小鸡,则需用篱笆的长是( )
如图所示,刘伯伯家有一块等边三角形的空地,已知E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围起来放养小鸡,则需用篱笆的长是( )| A. | 15米 | B. | 20米 | C. | 25米 | D. | 30米 |
18.若a,b,c为常数,且(a-c)2>a2+c2,则关于x的一元二次方程ax2+bx+c=0根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 有一个根或两个不相等的实数根 |
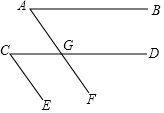 已知,如图:AB∥CD,若∠A的度数是x度,∠C的度数是y度,且x,y满足x2+y2=2xy,CE∥AF吗?为什么?
已知,如图:AB∥CD,若∠A的度数是x度,∠C的度数是y度,且x,y满足x2+y2=2xy,CE∥AF吗?为什么? 如图,△ABC为直角三角形,∠B=90°,AC边上取一点D,使CD=AB,分别过点C作CE⊥BC,过D作DE⊥AC,CE,DE相交于E.连结AE.
如图,△ABC为直角三角形,∠B=90°,AC边上取一点D,使CD=AB,分别过点C作CE⊥BC,过D作DE⊥AC,CE,DE相交于E.连结AE.