题目内容
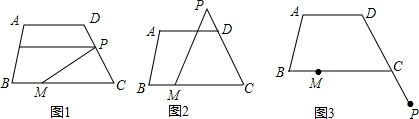
如图,四边形ABCD中,AD∥BC,∠ADC=120°,P为直线CD上一动点,点M在线段BC上,连MP,设∠MPD=α.
(1)如图1,若MP⊥CD,则∠BMP= 度;
(2)如图2,当P点在CD延长线上时,∠BMP= (用α表示);
(3)如图3,当P点在DC延长线上时,(2)中结论是否仍成立?请画出图形并证明你的判断.
(1)如图1,若MP⊥CD,则∠BMP=
(2)如图2,当P点在CD延长线上时,∠BMP=
(3)如图3,当P点在DC延长线上时,(2)中结论是否仍成立?请画出图形并证明你的判断.

考点:平行线的性质
专题:
分析:(1)根据两直线平行,同旁内角互补求出∠C,然后利用三角形的内角和定理求出∠CMP,再根据平角的定义列式计算即可得解;
(2)根据两直线平行,同旁内角互补求出∠C,然后利用三角形的内角和定理求出∠CMP,再根据平角的定义列式计算即可得解;
(3)根据两直线平行,同位角相等∠BCP,然后利用三角形的内角和定理求出∠CMP,再根据平角的定义列式计算即可得解.
(2)根据两直线平行,同旁内角互补求出∠C,然后利用三角形的内角和定理求出∠CMP,再根据平角的定义列式计算即可得解;
(3)根据两直线平行,同位角相等∠BCP,然后利用三角形的内角和定理求出∠CMP,再根据平角的定义列式计算即可得解.
解答:
 解:(1)∵AD∥BC,
解:(1)∵AD∥BC,
∴∠C=180°-∠ADC=180°-120°=60°,
∵MP⊥CD,
∴∠CMP=90°-∠C=90°-60°=30°,
∴∠BMP=180°-∠CMP=180°-30°=150°;
(2)∵AD∥BC,
∴∠C=180°-∠ADC=180°-120°=60°,
在△CMP中,∠CMP=180°-∠C-∠MPD=180°-60°-α=120°-α,
∴∠BMP=180°-∠CMP=180°-(120°-α)=60°+α;
故答案为:(1)150;(2)60°+α;
(3)不成立.
理由如下:∵AD∥BC,
∴∠BCP=∠ADC=120°,
在△CMP中,∠CMP=180°-∠BCP-∠MPD=180°-120°-α=60°-α,
∴∠BMP=180°-∠CMP=180°-(60°-α)=120°+α.
 解:(1)∵AD∥BC,
解:(1)∵AD∥BC,∴∠C=180°-∠ADC=180°-120°=60°,
∵MP⊥CD,
∴∠CMP=90°-∠C=90°-60°=30°,
∴∠BMP=180°-∠CMP=180°-30°=150°;
(2)∵AD∥BC,
∴∠C=180°-∠ADC=180°-120°=60°,
在△CMP中,∠CMP=180°-∠C-∠MPD=180°-60°-α=120°-α,
∴∠BMP=180°-∠CMP=180°-(120°-α)=60°+α;
故答案为:(1)150;(2)60°+α;
(3)不成立.
理由如下:∵AD∥BC,
∴∠BCP=∠ADC=120°,
在△CMP中,∠CMP=180°-∠BCP-∠MPD=180°-120°-α=60°-α,
∴∠BMP=180°-∠CMP=180°-(60°-α)=120°+α.
点评:本题考查了平行线的性质,三角形的内角和定理,平角的定义,是基础题,熟记性质并准确识图理清图中各角度之间的关系是解题的关键.

练习册系列答案
相关题目
若不等式(a+1)x>2的解集为x<
,则a的取值范围是( )
| 2 |
| a+1 |
| A、a<1 | B、a>1 |
| C、a<-1 | D、a>-1 |
一个学生随手写下了一串数字21221222122221,则2出现的频率是( )
| A、14 | ||
| B、10 | ||
C、
| ||
D、
|
下列运算正确的是( )
| A、a2+a4=a6 |
| B、2a×4a=8a |
| C、(a2)3=a6 |
| D、a6÷a3=a2 |
 如图所示,MN⊥b,ME⊥a,且MN=4cm,ME=6cm,则点M到直线b的距离是多少?
如图所示,MN⊥b,ME⊥a,且MN=4cm,ME=6cm,则点M到直线b的距离是多少?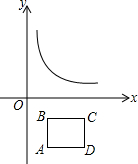 如图,矩形ABCD的边AB=2,BC=4,且BC∥x轴,已知点A的坐标是(2,4).
如图,矩形ABCD的边AB=2,BC=4,且BC∥x轴,已知点A的坐标是(2,4). 如图,∠1+∠C=100°,∠2+∠B=100°,AB与CD平行吗?说明你的理由.
如图,∠1+∠C=100°,∠2+∠B=100°,AB与CD平行吗?说明你的理由.