题目内容
19.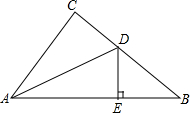 如图,在△ABC中,∠C=90°,AC=6,BC=8,AB=10,AD平分∠BAC交BC于点D,DE⊥AB于E,则CD的长度为( )
如图,在△ABC中,∠C=90°,AC=6,BC=8,AB=10,AD平分∠BAC交BC于点D,DE⊥AB于E,则CD的长度为( )| A. | 2cm | B. | 4cm | C. | 6cm | D. | 3cm |
分析 根据角平分线上的点到角的两边距离相等可得CD=DE,再利用“HL”证明Rt△ACD和Rt△AED全等,根据全等三角形对应边相等可得AE=AC,再利用勾股定理列式求出AB,然后求出BE,设CD=DE=x,表示出BD,然后利用勾股定理列出方程求解即可.
解答  解:过点D作DE⊥AB于E,
解:过点D作DE⊥AB于E,
∵AD平分∠BAC,
∴CD=DE,
在Rt△ACD和Rt△AED中,
$\left\{\begin{array}{l}{AD=AD}\\{CD=DE}\end{array}\right.$,
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC=6,
∴BE=AB-AE=10-6=4,
设CD=DE=x,则BD=8-x,
在Rt△BDE中,DE2+BE2=BD2,
x2+42=(8-x)2,
解得x=3,
即CD的长为3.
故选:D.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,熟记性质并利用勾股定理列出方程是解题的关键.

练习册系列答案
相关题目
4.下列根据等式的性质正确变形的是( )
| A. | 由-$\frac{1}{3}$x=$\frac{2}{3}$y,得x=2y | B. | 由3x-2=2x+2,得3x-2x=2+2 | ||
| C. | 由2x-3=3x,得2x-3x=-3 | D. | 由3x-5=7,得3x=7-5 |
9.若关于x的一元二次方程为ax2+bx+5=0(a≠0)的解是x=1,则2016-a-b的值是( )
| A. | 2018 | B. | 2011 | C. | 2014 | D. | 2021 |




 如图.已知矩形ABCD中,在BC上取一点E.沿AE将△ABE向上折叠.使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD:AB=(1+$\sqrt{5}$):2.
如图.已知矩形ABCD中,在BC上取一点E.沿AE将△ABE向上折叠.使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD:AB=(1+$\sqrt{5}$):2.