题目内容
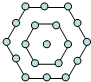 有一个形如六边形的点阵体操队形,它的中心是一个点,代表一个队员,算第一层,第二层每边有两个点,代表两个队员,共有6个队员,第三层每边有三个点,代表三个队员,共有12个队员,依此类推.用含n的代数式表示第n层的队员数是
有一个形如六边形的点阵体操队形,它的中心是一个点,代表一个队员,算第一层,第二层每边有两个点,代表两个队员,共有6个队员,第三层每边有三个点,代表三个队员,共有12个队员,依此类推.用含n的代数式表示第n层的队员数是考点:规律型:图形的变化类
专题:
分析:由于第二层每边有2个点,第三层每边有3个点…,则第二层的六边形点阵的总点数6×2-6=6,第三层的六边形点阵的总点数6×3-6=12,第四层的六边形点阵的总点数6×4-6=18,…,可得到每层总点数等于本层的层数的6倍与6的差,则第n(n>1)层的六边形点阵的总点数6n-6.
解答:解:第二层的六边形点阵的总点数6×2-6=6,
第三层的六边形点阵的总点数6×3-6=12,
第四层的六边形点阵的总点数6×4-6=18,
…
第n(n>1)层的六边形点阵的总点数6×n-6=6n-6.
故答案为:6n-6.
第三层的六边形点阵的总点数6×3-6=12,
第四层的六边形点阵的总点数6×4-6=18,
…
第n(n>1)层的六边形点阵的总点数6×n-6=6n-6.
故答案为:6n-6.
点评:此题考查图形的变化规律,通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.

练习册系列答案
相关题目
 在如图所示的面板上,有左右两组按钮,每组按钮中的两个按钮均分别控制一个灯泡和一个发音装置,同时按下两组中各一个按钮:当两个灯泡都亮时闯关成功;当按错一个按钮时,发音装置就会发出“闯关失败”的声音.1-4的四个按钮上分别写与四组算式:
在如图所示的面板上,有左右两组按钮,每组按钮中的两个按钮均分别控制一个灯泡和一个发音装置,同时按下两组中各一个按钮:当两个灯泡都亮时闯关成功;当按错一个按钮时,发音装置就会发出“闯关失败”的声音.1-4的四个按钮上分别写与四组算式: 如图,A为⊙O外一点,AO交⊙O于点P,AB切⊙O于点B,AP=5厘米,AB=5
如图,A为⊙O外一点,AO交⊙O于点P,AB切⊙O于点B,AP=5厘米,AB=5