题目内容
在同一平面内的n条直线两两相交,最多共有28个交点,则n= .
考点:规律型:图形的变化类
专题:推理填空题
分析:从简单情形考虑:分别求出2条、3条、4条、5条、6条直线相交时最多的交点个数,找出规律即可解答.
解答:解:2条直线相交最多有1个交点;
3条直线相交最多有1+2个交点;
4条直线相交最多有1+2+3个交点;
5条直线相交最多有1+2+3+4个交点;
6条直线相交最多有1+2+3+4+5个交点;
…
所以n条直线相交最多有1+2+3+4+5+…+(n-1)=
个交点;
由题意得
=28,
解得n=8.
故答案为:8.
3条直线相交最多有1+2个交点;
4条直线相交最多有1+2+3个交点;
5条直线相交最多有1+2+3+4个交点;
6条直线相交最多有1+2+3+4+5个交点;
…
所以n条直线相交最多有1+2+3+4+5+…+(n-1)=
| n(n-1) |
| 2 |
由题意得
| n(n-1) |
| 2 |
解得n=8.
故答案为:8.
点评:此题考查图形的变化规律,解答此题的关键是找出其中的规律,利用规律解决问题.

练习册系列答案
相关题目
下列各式符合代数式书写规范的是( )
A、2
| ||
| B、a×3 | ||
| C、a÷b | ||
| D、3x-1 |
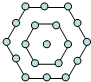 有一个形如六边形的点阵体操队形,它的中心是一个点,代表一个队员,算第一层,第二层每边有两个点,代表两个队员,共有6个队员,第三层每边有三个点,代表三个队员,共有12个队员,依此类推.用含n的代数式表示第n层的队员数是
有一个形如六边形的点阵体操队形,它的中心是一个点,代表一个队员,算第一层,第二层每边有两个点,代表两个队员,共有6个队员,第三层每边有三个点,代表三个队员,共有12个队员,依此类推.用含n的代数式表示第n层的队员数是