题目内容
 如图,A为⊙O外一点,AO交⊙O于点P,AB切⊙O于点B,AP=5厘米,AB=5
如图,A为⊙O外一点,AO交⊙O于点P,AB切⊙O于点B,AP=5厘米,AB=5| 3 |
考点:切线的性质,扇形面积的计算
专题:
分析:首先连接OB,由AB切⊙O于点B,可得OB⊥AB,然后设⊙O的半径为xcm,由勾股定理即可求得x2+(5
)2=(x+5)2,解此方程即可求得⊙O的半径,又由S阴影=S△AOB-S扇形OBP,即可求得答案.
| 3 |
解答: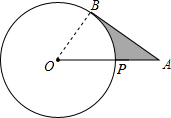 解:连接OB,
解:连接OB,
∵AB切⊙O于点B,
∴OB⊥AB,
∴∠ABO=90°,
设⊙O的半径为xcm,则OB=xcm,OA=AP+OP=5+x(cm),
∵OB2+AB2=OA2,
∴x2+(5
)2=(x+5)2,
解得:x=5,
∴OB=5cm,OA=10cm,
∴∠A=30°,
∴∠AOB=60°,
∴S阴影=S△AOB-S扇形OBP=
×5×5
-
=
-
.
 解:连接OB,
解:连接OB,∵AB切⊙O于点B,
∴OB⊥AB,
∴∠ABO=90°,
设⊙O的半径为xcm,则OB=xcm,OA=AP+OP=5+x(cm),
∵OB2+AB2=OA2,
∴x2+(5
| 3 |
解得:x=5,
∴OB=5cm,OA=10cm,
∴∠A=30°,
∴∠AOB=60°,
∴S阴影=S△AOB-S扇形OBP=
| 1 |
| 2 |
| 3 |
| 60×π×52 |
| 360 |
25
| ||
| 2 |
| 25π |
| 6 |
点评:此题考查了切线的性质以及勾股定理.此题难度不大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
若非零实数a、b满足a2+4b2=4ab,则
的值为( )
| a |
| b |
| A、-2 | ||
| B、2 | ||
C、
| ||
D、-
|
下列图形具有稳定性的是( )
| A、正三角形 | B、正方形 |
| C、正五边形 | D、正六边形 |
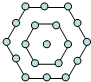 有一个形如六边形的点阵体操队形,它的中心是一个点,代表一个队员,算第一层,第二层每边有两个点,代表两个队员,共有6个队员,第三层每边有三个点,代表三个队员,共有12个队员,依此类推.用含n的代数式表示第n层的队员数是
有一个形如六边形的点阵体操队形,它的中心是一个点,代表一个队员,算第一层,第二层每边有两个点,代表两个队员,共有6个队员,第三层每边有三个点,代表三个队员,共有12个队员,依此类推.用含n的代数式表示第n层的队员数是