题目内容
9. 如图,已知AB是半圆O直径,C为半圆上一点,CD切半圆于C,AD⊥CD于D,以C为圆心,CD为半径为⊙C,求证:AB是⊙C的切线.
如图,已知AB是半圆O直径,C为半圆上一点,CD切半圆于C,AD⊥CD于D,以C为圆心,CD为半径为⊙C,求证:AB是⊙C的切线.
分析 作CE⊥AB,连接AC、OC,由CD切半圆于C知OC⊥CD,结合AD⊥CD知AD∥OC,从而证得∠DAC=∠EAC,再证△DAC≌△EAC得CE=CD,即CE为⊙C的半径,即可得证.
解答 证明:如图,过点C作CE⊥AB于点E,连接AC、OC,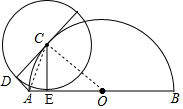
∵CD切半圆于C,
∴OC⊥CD,
又∵AD⊥CD,
∴AD∥OC,
∴∠OCA=∠DAC,
∵∠OCA=∠OAC,
∴∠DAC=∠EAC,
∵CE⊥AB,
∴∠CEA=∠CDA=90°,
在△DAC和△EAC中,
∵$\left\{\begin{array}{l}{∠CDA=∠CEA}\\{∠CAD=∠CAE}\\{AC=AC}\end{array}\right.$,
∴△DAC≌△EAC,
∴CE=CD,即CE为⊙C的半径,
∴AB是⊙C的切线.
点评 本题主要考查切线的判定与性质、全等三角形的判定与性质等,作垂直证半径是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
14.把抛物线y=x2+1向左平移3个单位,再向下平移2个单位,得到的抛物线的顶点为( )
| A. | (3,-1) | B. | (3,1) | C. | (-3,1) | D. | (-3,-1) |
 如图,在Rt△ABC中,∠C=90°,AC=12cm,BC=6cm,一条线段PQ=AB,P,Q两点分别在线段AC和AC的垂线AX上移动,则当AP=6cm或12cm时,才能使△ABC和△APQ全等.
如图,在Rt△ABC中,∠C=90°,AC=12cm,BC=6cm,一条线段PQ=AB,P,Q两点分别在线段AC和AC的垂线AX上移动,则当AP=6cm或12cm时,才能使△ABC和△APQ全等. 如图,在Rt△ABC中,∠C=90°,∠B=60°,将△ABC绕点A逆时针旋转60°,点B、C分别落在点B'、C'处,联结BC'与AC边交于点D,那么$\frac{BD}{DC'}$=$\frac{2}{3}$.
如图,在Rt△ABC中,∠C=90°,∠B=60°,将△ABC绕点A逆时针旋转60°,点B、C分别落在点B'、C'处,联结BC'与AC边交于点D,那么$\frac{BD}{DC'}$=$\frac{2}{3}$.
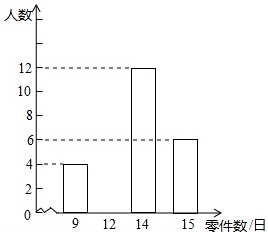 某车间有120名工人,为了了解这些工人日加工零件数的情况,随机抽出其中的30名工人调查,整理调查结果,绘制出不完整的条形统计图(如图).根据图中的信息,解答下列问题:
某车间有120名工人,为了了解这些工人日加工零件数的情况,随机抽出其中的30名工人调查,整理调查结果,绘制出不完整的条形统计图(如图).根据图中的信息,解答下列问题: 如图,△ABC中,∠B=22.5°,AB的垂直平分线交BC于D,AE⊥BC于E,DF⊥AC于F,与AE交于点G.
如图,△ABC中,∠B=22.5°,AB的垂直平分线交BC于D,AE⊥BC于E,DF⊥AC于F,与AE交于点G.