题目内容
19.若关于x、y的二元一次方程组$\left\{\begin{array}{l}{2x+y=-3m+2}\\{x+2y=4}\end{array}\right.$的解满足$x+y>\frac{1}{2}$,则满足条件的m的所有正整数值是( )| A. | 1,2,3,4 | B. | 1,2,3 | C. | 1,2 | D. | 1 |
分析 方程组两方程相加表示出x+y,代入所求不等式计算确定出m的范围,即可确定出m的正整数值.
解答 解:$\left\{\begin{array}{l}{2x+y=-3m+2①}\\{x+2y=4②}\end{array}\right.$,
①+②得:3(x+y)=-3m+6,
解得:x+y=-m+2,
代入得:-m+2>$\frac{1}{2}$,
解得:m<$\frac{3}{2}$,
则满足条件的m的所有正整数值是1,
故选D
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
相关题目
9.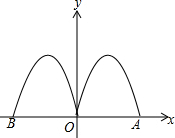 如图,抛物线y=-2x2+4x与x轴交于点O、A,把抛物线在x轴及其上方的部分记为C1,将C1以y铀为对称轴作轴对称得到C2,C2与x轴交于点B,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是( )
如图,抛物线y=-2x2+4x与x轴交于点O、A,把抛物线在x轴及其上方的部分记为C1,将C1以y铀为对称轴作轴对称得到C2,C2与x轴交于点B,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是( )
 如图,抛物线y=-2x2+4x与x轴交于点O、A,把抛物线在x轴及其上方的部分记为C1,将C1以y铀为对称轴作轴对称得到C2,C2与x轴交于点B,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是( )
如图,抛物线y=-2x2+4x与x轴交于点O、A,把抛物线在x轴及其上方的部分记为C1,将C1以y铀为对称轴作轴对称得到C2,C2与x轴交于点B,若直线y=x+m与C1,C2共有3个不同的交点,则m的取值范围是( )| A. | 0<m$<\frac{9}{8}$ | B. | $\frac{9}{8}$<m<$\frac{25}{8}$ | C. | 0<m<$\frac{25}{8}$ | D. | m<$\frac{9}{8}$或m<$\frac{25}{8}$ |
10.下列成语所描述的事件是必然事件的是( )
| A. | 瓮中捉鳖 | B. | 守株待兔 | C. | 拔苗助长 | D. | 水中捞月 |
7.同样大小的黑色棋子按如图所示的规律摆放:

那么第671个图形中棋子的个数为( )

那么第671个图形中棋子的个数为( )
| A. | 2016 | B. | 2015 | C. | 2014 | D. | 2013 |
14.我国最长的河流长江全长约为6300千米,数6300用科学记数法表示为( )
| A. | 0.63×104 | B. | 6.3×103 | C. | 63×102 | D. | 6.3×106 |
4. 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=$\frac{1}{2}$,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③a-b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=$\frac{1}{2}$,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③a-b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=$\frac{1}{2}$,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③a-b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=$\frac{1}{2}$,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③a-b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )| A. | ①②③④ | B. | ③④ | C. | ①③④ | D. | ①② |
11.有四盒包装“行唐大枣”,每盒以标准克数(1000克)为基准,超过的克数记作正数,不足的克数记作负数,以下数据是记录结果,其中实际克数最接近标准克数的是( )
| A. | +8 | B. | -12 | C. | +13 | D. | -13 |
8. 如图是一个几何体的三视图,则这个几何体的侧面积是( )
如图是一个几何体的三视图,则这个几何体的侧面积是( )
 如图是一个几何体的三视图,则这个几何体的侧面积是( )
如图是一个几何体的三视图,则这个几何体的侧面积是( )| A. | 9π | B. | 18π | C. | 27π | D. | 36π |
 如图,在半圆BAC中,点O为圆心,OD⊥AB于D,OE⊥AC于E,连接DE,若DE=AB=2,则图中阴影部分的面积为2π-2$\sqrt{3}$(结果保留π)
如图,在半圆BAC中,点O为圆心,OD⊥AB于D,OE⊥AC于E,连接DE,若DE=AB=2,则图中阴影部分的面积为2π-2$\sqrt{3}$(结果保留π)